Question Number 28096 by tawa tawa last updated on 20/Jan/18
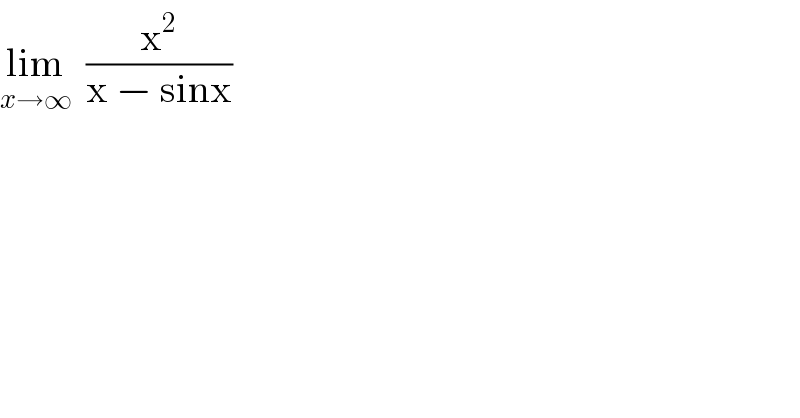
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\:\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{x}\:−\:\mathrm{sinx}} \\ $$
Commented by abdo imad last updated on 20/Jan/18
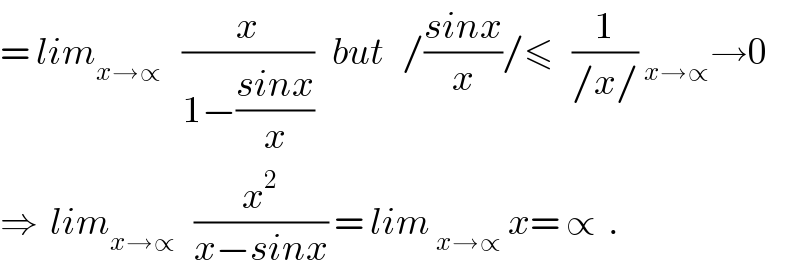
$$=\:{lim}_{{x}\rightarrow\propto\:\:} \:\:\frac{{x}}{\mathrm{1}−\frac{{sinx}}{{x}}}\:\:\:{but}\:\:\:/\frac{{sinx}}{{x}}/\leqslant\:\:\:\frac{\mathrm{1}}{/{x}/}\:_{{x}\rightarrow\propto} \rightarrow\mathrm{0} \\ $$$$\Rightarrow\:\:{lim}_{{x}\rightarrow\propto} \:\:\:\frac{{x}^{\mathrm{2}} }{{x}−{sinx}}\:=\:{lim}\:_{{x}\rightarrow\propto} \:{x}=\:\propto\:\:. \\ $$
Commented by tawa tawa last updated on 21/Jan/18

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
