Question Number 180106 by cherokeesay last updated on 07/Nov/22

$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\sqrt{{x}^{\mathrm{2}} +{x}}−{x} \\ $$
Answered by a.lgnaoui last updated on 07/Nov/22
![(√(x^2 +x)) −x=((((√(x^2 +x)) −x)((√(x^2 +x)) +x))/( (√(x^2 +x)) +x)) (x∈(]−∞,0]∪[−1,+∞[) =(x/( (√(x^2 +x)) +x)) =(x/(x((√(1+(1/x))) +1))) =(1/( (√(1+(1/x))) +1)) lim_(x→∞) (√(x^2 +x)) −x=lim_(x→∞) (1/( (√(1+(1/x))) +1))=(1/2)](https://www.tinkutara.com/question/Q180108.png)
$$\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}}\:−\mathrm{x}=\frac{\left(\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}}\:−\mathrm{x}\right)\left(\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}}\:+\mathrm{x}\right)}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}}\:+\mathrm{x}}\:\:\left(\mathrm{x}\in\left(\right]−\infty,\mathrm{0}\right]\cup\left[−\mathrm{1},+\infty\left[\right)\right. \\ $$$$=\frac{\mathrm{x}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}}\:+\mathrm{x}}\:=\frac{\mathrm{x}}{\mathrm{x}\left(\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}}}\:+\mathrm{1}\right)}\:\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}}}\:+\mathrm{1}} \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow\infty} \sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}}\:−\mathrm{x}=\mathrm{lim}_{\mathrm{x}\rightarrow\infty} \frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}}}\:+\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by cherokeesay last updated on 07/Nov/22

$${very}\:{nice}, \\ $$$${thank}\:{you}\:{sir}. \\ $$
Answered by CElcedricjunior last updated on 07/Nov/22

$$\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Answered by mr W last updated on 07/Nov/22
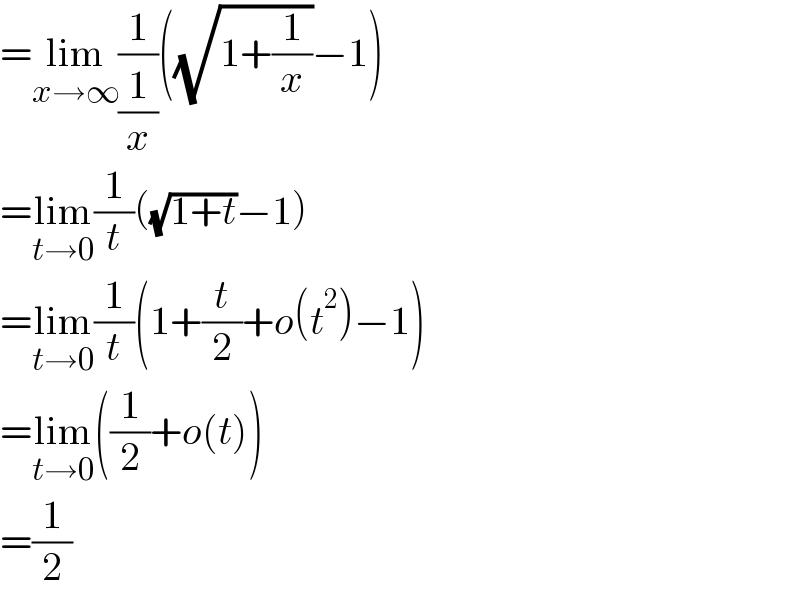
$$=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{\frac{\mathrm{1}}{{x}}}\left(\sqrt{\mathrm{1}+\frac{\mathrm{1}}{{x}}}−\mathrm{1}\right) \\ $$$$=\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}}{{t}}\left(\sqrt{\mathrm{1}+{t}}−\mathrm{1}\right) \\ $$$$=\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}}{{t}}\left(\mathrm{1}+\frac{{t}}{\mathrm{2}}+{o}\left({t}^{\mathrm{2}} \right)−\mathrm{1}\right) \\ $$$$=\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{1}}{\mathrm{2}}+{o}\left({t}\right)\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by cherokeesay last updated on 07/Nov/22

$${Nice},\:{thank}\:{you}\:{master}. \\ $$
