Question Number 83865 by jagoll last updated on 07/Mar/20
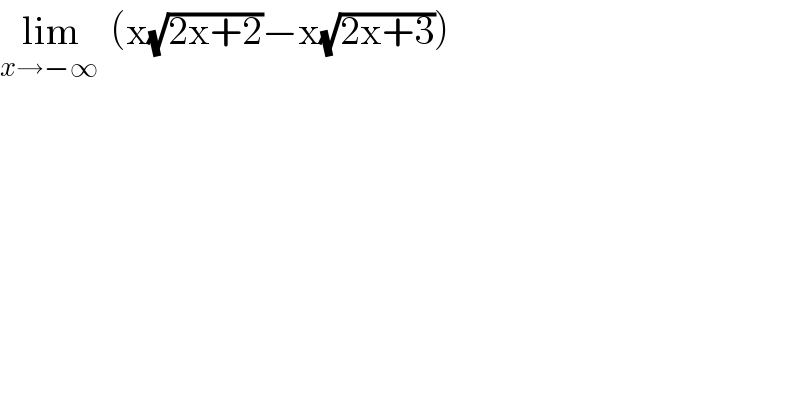
$$\underset{{x}\rightarrow−\infty\:} {\mathrm{lim}}\:\left(\mathrm{x}\sqrt{\mathrm{2x}+\mathrm{2}}−\mathrm{x}\sqrt{\mathrm{2x}+\mathrm{3}}\right) \\ $$
Commented by mr W last updated on 07/Mar/20

$$\mathrm{2}{x}+\mathrm{2}\geqslant\mathrm{0} \\ $$$$\Rightarrow{x}\geqslant−\mathrm{1} \\ $$$$\Rightarrow{for}\:{x}\rightarrow−\infty\:{function}\:{not}\:{defined}! \\ $$$${it}\:{should}\:{be}\:{x}\rightarrow+\infty! \\ $$$$\underset{{x}\rightarrow+\infty\:} {\mathrm{lim}}\:\left(\mathrm{x}\sqrt{\mathrm{2x}+\mathrm{2}}−\mathrm{x}\sqrt{\mathrm{2x}+\mathrm{3}}\right) \\ $$$$=\underset{{x}\rightarrow+\infty} {\mathrm{lim}}\frac{−{x}}{\:\sqrt{\mathrm{2}{x}+\mathrm{2}}+\sqrt{\mathrm{2}{x}+\mathrm{3}}} \\ $$$$=\underset{{x}\rightarrow+\infty} {\mathrm{lim}}\frac{−\sqrt{{x}}}{\:\sqrt{\mathrm{2}+\frac{\mathrm{2}}{{x}}}+\sqrt{\mathrm{2}+\frac{\mathrm{3}}{{x}}}} \\ $$$$=\underset{{x}\rightarrow+\infty} {\mathrm{lim}}\frac{−\infty}{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$$=−\infty \\ $$
Commented by jagoll last updated on 07/Mar/20

$$\mathrm{yes}\:\mathrm{sir}.\:\mathrm{it}\:\mathrm{impossible}\:\mathrm{for}\:\mathrm{x}\:\rightarrow−\infty \\ $$
Commented by mathmax by abdo last updated on 07/Mar/20

$${function}\:\:{not}\:{defined}\:{at}\:−\infty \\ $$$${at}\:+\infty\:\:{we}\:{have}\:\sqrt{\mathrm{2}{x}+\mathrm{2}}=\sqrt{\mathrm{2}{x}\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)}=\sqrt{\mathrm{2}{x}}\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$=\sqrt{\mathrm{2}{x}}\left\{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}}{{x}}\:+\frac{\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}\right)}{\mathrm{2}}×\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:+{o}\left(\frac{\mathrm{1}}{{x}^{\mathrm{3}} }\right)\right\} \\ $$$$=\sqrt{\mathrm{2}{x}}\left\{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}{x}}−\frac{\mathrm{1}}{\mathrm{8}{x}^{\mathrm{2}} }\:+{o}\left(\frac{\mathrm{1}}{{x}^{\mathrm{3}} }\right)\right\} \\ $$$$\sqrt{\mathrm{2}{x}+\mathrm{3}}=\sqrt{\mathrm{2}{x}\left(\mathrm{1}+\frac{\mathrm{3}}{\mathrm{2}{x}}\right)}=\sqrt{\mathrm{2}{x}}\left(\mathrm{1}+\frac{\mathrm{3}}{\mathrm{2}{x}}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \: \\ $$$$=\sqrt{\mathrm{2}{x}}\left\{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{3}}{\mathrm{2}{x}}\right)\:−\frac{\mathrm{1}}{\mathrm{8}}\left(\frac{\mathrm{3}}{\mathrm{2}{x}}\right)^{\mathrm{2}} \:+{o}\left(\frac{\mathrm{1}}{{x}^{\mathrm{3}} }\right)\right\} \\ $$$$=\sqrt{\mathrm{2}{x}}\left\{\mathrm{1}+\frac{\mathrm{3}}{\mathrm{4}{x}}−\frac{\mathrm{9}}{\mathrm{32}{x}^{\mathrm{2}} }\:+{o}\left(\frac{\mathrm{1}}{{x}^{\mathrm{3}} }\right)\right\}\:\Rightarrow \\ $$$${f}\left({x}\right)\sim\sqrt{\mathrm{2}{x}}\left({x}+\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{8}{x}}+{o}\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)\right)−\sqrt{\mathrm{2}{x}}\left({x}+\frac{\mathrm{3}}{\mathrm{4}}−\frac{\mathrm{9}}{\mathrm{32}{x}}\:+{o}\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)\right)\:\Rightarrow \\ $$$${f}\left({x}\right)\sim\sqrt{\mathrm{2}{x}}\left\{\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{3}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{8}{x}}+\frac{\mathrm{9}}{\mathrm{32}{x}}\:+{o}\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)\right)\:\Rightarrow \\ $$$${f}\left({x}\right)\sim−\frac{\mathrm{1}}{\mathrm{4}}\sqrt{\mathrm{2}{x}}−\frac{\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{8}\sqrt{{x}}}\:+\frac{\mathrm{9}\sqrt{\mathrm{2}}}{\mathrm{32}\sqrt{{x}}}\:\Rightarrow{lim}_{{x}\rightarrow+\infty} {f}\left({x}\right)=−\infty \\ $$
