Question Number 62539 by aliesam last updated on 22/Jun/19
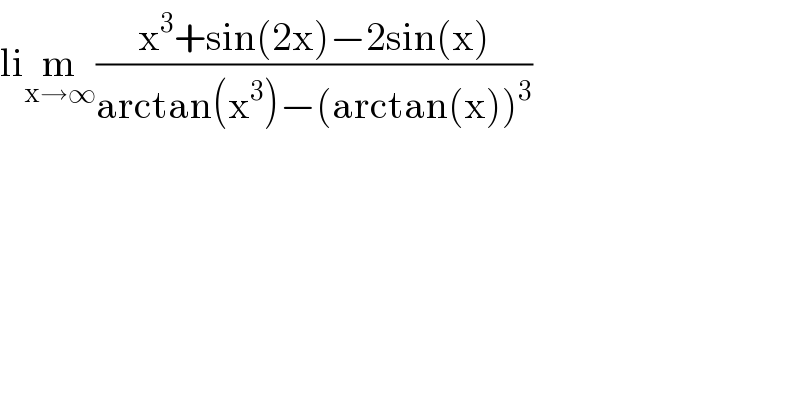
$$\mathrm{li}\underset{\mathrm{x}\rightarrow\infty} {\mathrm{m}}\frac{\mathrm{x}^{\mathrm{3}} +\mathrm{sin}\left(\mathrm{2x}\right)−\mathrm{2sin}\left(\mathrm{x}\right)}{\mathrm{arctan}\left(\mathrm{x}^{\mathrm{3}} \right)−\left(\mathrm{arctan}\left(\mathrm{x}\right)\right)^{\mathrm{3}} } \\ $$
Answered by tanmay last updated on 22/Jun/19
![lim_(x→0) ((x^3 +(2x−((8x^3 )/(3!))+((32x^5 )/(5!)))−2(x−(x^3 /(3!))+(x^5 /(5!))))/((x^3 −(x^9 /3))−(x−(x^3 /3))^3 )) lim_(x→0) ((x^3 −((8x^3 )/(3!))+((2x^3 )/(3!))+((32x^5 )/(5!))−((2x^5 )/(5!)))/(x^3 −(x^9 /3)−x^3 +3x^2 ×(x^3 /3)−3x×(x^6 /9)+(x^9 /(27)))) lim_(x→0) ((x^3 (1+(2/(3!))−(8/(3!)))+(x^5 /(5!))(32−2))/(((−x^9 )/3)+x^5 −(x^7 /3)+(x^9 /(27)))) lim_(x→0) (((30)/(120))/(((−x^4 )/3)+1−(x^2 /3)+(x^4 /(27)))) =(1/4) [deviding N_r and D_r by x^5 ] i think lim_(x→0) not lim_(x→∞) li_(x→∞)](https://www.tinkutara.com/question/Q62546.png)
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}^{\mathrm{3}} +\left(\mathrm{2}{x}−\frac{\mathrm{8}{x}^{\mathrm{3}} }{\mathrm{3}!}+\frac{\mathrm{32}{x}^{\mathrm{5}} }{\mathrm{5}!}\right)−\mathrm{2}\left({x}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}+\frac{{x}^{\mathrm{5}} }{\mathrm{5}!}\right)}{\left({x}^{\mathrm{3}} −\frac{{x}^{\mathrm{9}} }{\mathrm{3}}\right)−\left({x}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}}\right)^{\mathrm{3}} } \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}^{\mathrm{3}} −\frac{\mathrm{8}{x}^{\mathrm{3}} }{\mathrm{3}!}+\frac{\mathrm{2}{x}^{\mathrm{3}} }{\mathrm{3}!}+\frac{\mathrm{32}{x}^{\mathrm{5}} }{\mathrm{5}!}−\frac{\mathrm{2}{x}^{\mathrm{5}} }{\mathrm{5}!}}{{x}^{\mathrm{3}} −\frac{{x}^{\mathrm{9}} }{\mathrm{3}}−{x}^{\mathrm{3}} +\mathrm{3}{x}^{\mathrm{2}} ×\frac{{x}^{\mathrm{3}} }{\mathrm{3}}−\mathrm{3}{x}×\frac{{x}^{\mathrm{6}} }{\mathrm{9}}+\frac{{x}^{\mathrm{9}} }{\mathrm{27}}} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}^{\mathrm{3}} \left(\mathrm{1}+\frac{\mathrm{2}}{\mathrm{3}!}−\frac{\mathrm{8}}{\mathrm{3}!}\right)+\frac{{x}^{\mathrm{5}} }{\mathrm{5}!}\left(\mathrm{32}−\mathrm{2}\right)}{\frac{−{x}^{\mathrm{9}} }{\mathrm{3}}+{x}^{\mathrm{5}} −\frac{{x}^{\mathrm{7}} }{\mathrm{3}}+\frac{{x}^{\mathrm{9}} }{\mathrm{27}}} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\:\:\:\frac{\frac{\mathrm{30}}{\mathrm{120}}}{\frac{−{x}^{\mathrm{4}} }{\mathrm{3}}+\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{3}}+\frac{{x}^{\mathrm{4}} }{\mathrm{27}}}\:=\frac{\mathrm{1}}{\mathrm{4}}\:\left[{deviding}\:{N}_{{r}} {and}\:{D}_{{r}} {by}\:{x}^{\mathrm{5}} \right] \\ $$$$ \\ $$$${i}\:{think}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:{not}\:\underset{{x}\rightarrow\infty} {\mathrm{lim}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{li}} \\ $$$$ \\ $$
Commented by aliesam last updated on 22/Jun/19
$$\mathrm{yes}\:\mathrm{sir}\:\mathrm{its}\:\mathrm{typo}\:\mathrm{so}\:\mathrm{sorry} \\ $$
