Question Number 15186 by Joel577 last updated on 08/Jun/17
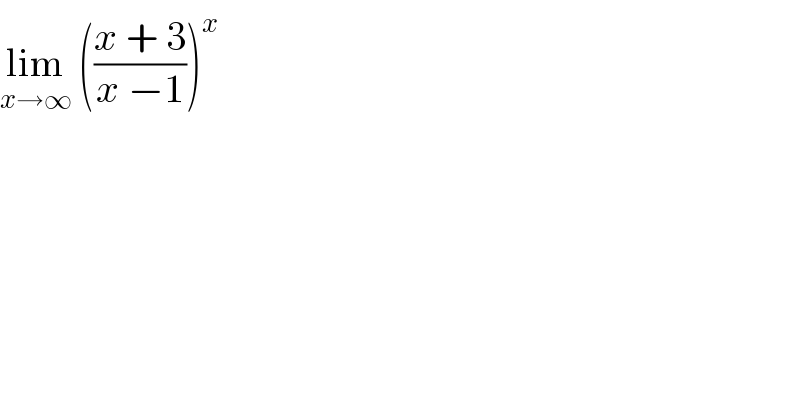
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left(\frac{{x}\:+\:\mathrm{3}}{{x}\:−\mathrm{1}}\right)^{{x}} \\ $$
Commented by mrW1 last updated on 08/Jun/17

$$\mathrm{yes},\:\mathrm{correct}. \\ $$
Commented by Joel577 last updated on 08/Jun/17
$${thank}\:{you}\:{very}\:{much} \\ $$
Commented by Joel577 last updated on 08/Jun/17
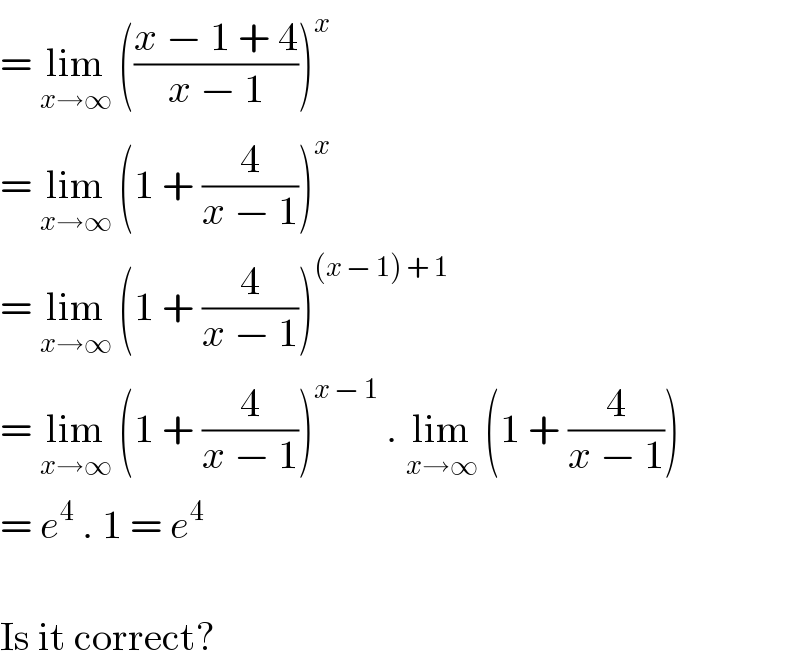
$$=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left(\frac{{x}\:−\:\mathrm{1}\:+\:\mathrm{4}}{{x}\:−\:\mathrm{1}}\right)^{{x}} \\ $$$$=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left(\mathrm{1}\:+\:\frac{\mathrm{4}}{{x}\:−\:\mathrm{1}}\right)^{{x}} \\ $$$$=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left(\mathrm{1}\:+\:\frac{\mathrm{4}}{{x}\:−\:\mathrm{1}}\right)^{\left({x}\:−\:\mathrm{1}\right)\:+\:\mathrm{1}} \\ $$$$=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left(\mathrm{1}\:+\:\frac{\mathrm{4}}{{x}\:−\:\mathrm{1}}\right)^{{x}\:−\:\mathrm{1}} \:.\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left(\mathrm{1}\:+\:\frac{\mathrm{4}}{{x}\:−\:\mathrm{1}}\right) \\ $$$$=\:{e}^{\mathrm{4}} \:.\:\mathrm{1}\:=\:{e}^{\mathrm{4}} \\ $$$$ \\ $$$$\mathrm{Is}\:\mathrm{it}\:\mathrm{correct}? \\ $$
