Question Number 128185 by liberty last updated on 05/Jan/21

$$\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\mathrm{x}+\mathrm{3}}{\mathrm{x}−\mathrm{1}}\right)^{\mathrm{x}+\mathrm{3}} \:=?\: \\ $$
Answered by john_santu last updated on 05/Jan/21
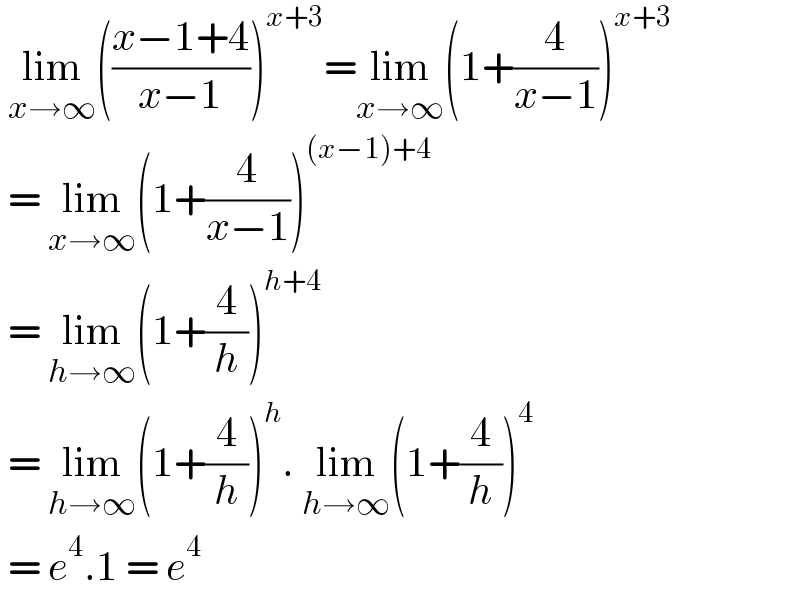
$$\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\frac{{x}−\mathrm{1}+\mathrm{4}}{{x}−\mathrm{1}}\right)^{{x}+\mathrm{3}} =\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{1}+\frac{\mathrm{4}}{{x}−\mathrm{1}}\right)^{{x}+\mathrm{3}} \\ $$$$\:=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{1}+\frac{\mathrm{4}}{{x}−\mathrm{1}}\right)^{\left({x}−\mathrm{1}\right)+\mathrm{4}} \\ $$$$\:=\:\underset{{h}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{1}+\frac{\mathrm{4}}{{h}}\right)^{{h}+\mathrm{4}} \:\: \\ $$$$\:=\:\underset{{h}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{1}+\frac{\mathrm{4}}{{h}}\right)^{{h}} .\:\underset{{h}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{1}+\frac{\mathrm{4}}{{h}}\right)^{\mathrm{4}} \\ $$$$\:=\:{e}^{\mathrm{4}} .\mathrm{1}\:=\:{e}^{\mathrm{4}} \: \\ $$
