Question Number 112900 by bemath last updated on 10/Sep/20
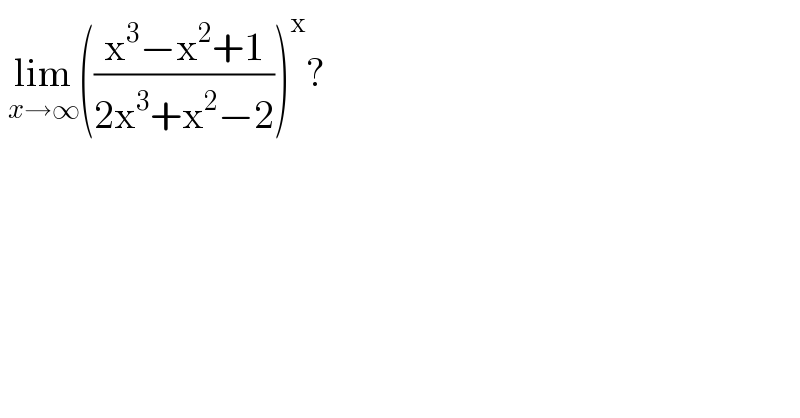
$$\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\mathrm{x}^{\mathrm{3}} −\mathrm{x}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2x}^{\mathrm{3}} +\mathrm{x}^{\mathrm{2}} −\mathrm{2}}\right)^{\mathrm{x}} ? \\ $$
Commented by kaivan.ahmadi last updated on 10/Sep/20
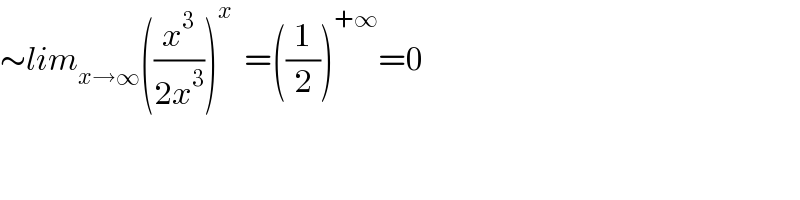
$$\sim{lim}_{{x}\rightarrow\infty} \left(\frac{{x}^{\mathrm{3}} }{\mathrm{2}{x}^{\mathrm{3}} }\right)^{{x}} \:\:=\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{+\infty} =\mathrm{0} \\ $$
Answered by mathmax by abdo last updated on 10/Sep/20
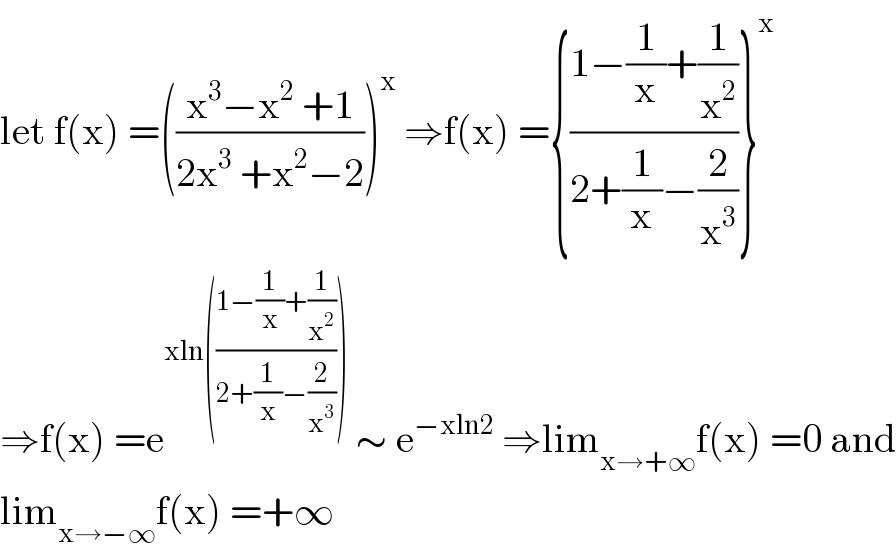
$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)\:=\left(\frac{\mathrm{x}^{\mathrm{3}} −\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}{\mathrm{2x}^{\mathrm{3}} \:+\mathrm{x}^{\mathrm{2}} −\mathrm{2}}\right)^{\mathrm{x}} \:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\:=\left\{\frac{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{x}}+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }}{\mathrm{2}+\frac{\mathrm{1}}{\mathrm{x}}−\frac{\mathrm{2}}{\mathrm{x}^{\mathrm{3}} }}\right\}^{\mathrm{x}} \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{e}^{\mathrm{xln}\left(\frac{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{x}}+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }}{\mathrm{2}+\frac{\mathrm{1}}{\mathrm{x}}−\frac{\mathrm{2}}{\mathrm{x}^{\mathrm{3}} }}\right)} \:\sim\:\mathrm{e}^{−\mathrm{xln2}} \:\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{0}\:\mathrm{and} \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow−\infty} \mathrm{f}\left(\mathrm{x}\right)\:=+\infty \\ $$
