Question Number 119977 by bramlexs22 last updated on 28/Oct/20
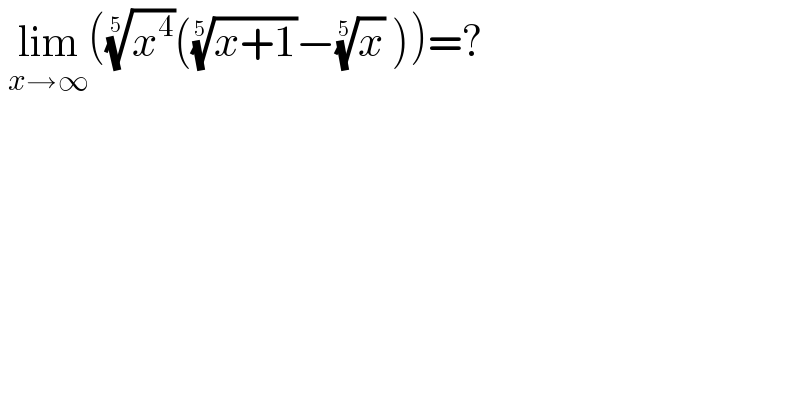
$$\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\sqrt[{\mathrm{5}}]{{x}^{\mathrm{4}} }\left(\sqrt[{\mathrm{5}}]{{x}+\mathrm{1}}−\sqrt[{\mathrm{5}}]{{x}}\:\right)\right)=? \\ $$
Answered by bemath last updated on 28/Oct/20
![lim_(x→∞) ((x^5 +x^4 ))^(1/5) −(x^5 )^(1/5) = lim_(x→∞) x ((1+(1/x)))^(1/5) −x [ let (1/x) = v ] lim_(v→0) ((((1+v))^(1/5) −1)/v) = lim_(v→0) (((1+(v/5))−1)/v) = (1/5)](https://www.tinkutara.com/question/Q119980.png)
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\sqrt[{\mathrm{5}}]{{x}^{\mathrm{5}} +{x}^{\mathrm{4}} }−\sqrt[{\mathrm{5}}]{{x}^{\mathrm{5}} }\:=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:{x}\:\sqrt[{\mathrm{5}}]{\mathrm{1}+\frac{\mathrm{1}}{{x}}}−{x}\: \\ $$$$\left[\:{let}\:\frac{\mathrm{1}}{{x}}\:=\:{v}\:\right]\: \\ $$$$\underset{{v}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt[{\mathrm{5}}]{\mathrm{1}+{v}}−\mathrm{1}}{{v}}\:=\:\underset{{v}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{1}+\frac{{v}}{\mathrm{5}}\right)−\mathrm{1}}{{v}}\:=\:\frac{\mathrm{1}}{\mathrm{5}} \\ $$
Answered by Dwaipayan Shikari last updated on 28/Oct/20
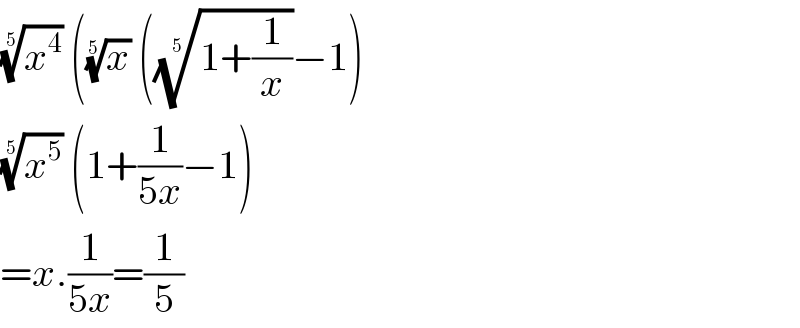
$$\sqrt[{\mathrm{5}}]{{x}^{\mathrm{4}} }\:\left(\sqrt[{\mathrm{5}}]{{x}}\:\left(\sqrt[{\mathrm{5}}]{\mathrm{1}+\frac{\mathrm{1}}{{x}}}−\mathrm{1}\right)\right. \\ $$$$\sqrt[{\mathrm{5}}]{{x}^{\mathrm{5}} }\:\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{5}{x}}−\mathrm{1}\right) \\ $$$$={x}.\frac{\mathrm{1}}{\mathrm{5}{x}}=\frac{\mathrm{1}}{\mathrm{5}} \\ $$
