Question Number 184859 by mnjuly1970 last updated on 12/Jan/23
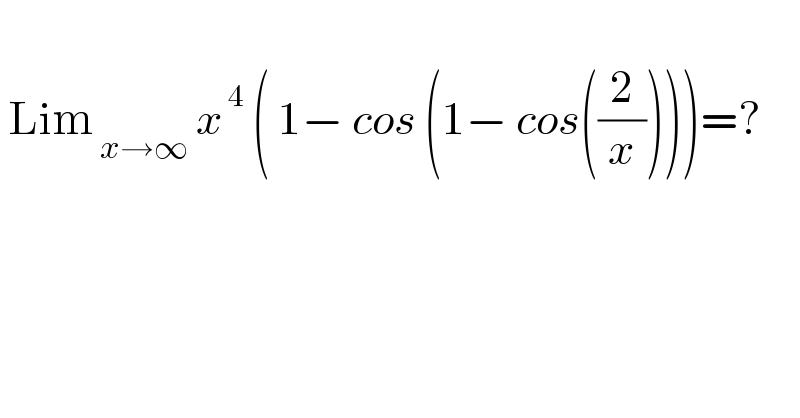
$$ \\ $$$$\:\mathrm{Lim}_{\:{x}\rightarrow\infty} \:{x}^{\:\mathrm{4}} \:\left(\:\mathrm{1}−\:{cos}\:\left(\mathrm{1}−\:{cos}\left(\frac{\mathrm{2}}{{x}}\right)\right)\right)=? \\ $$$$ \\ $$
Answered by qaz last updated on 12/Jan/23
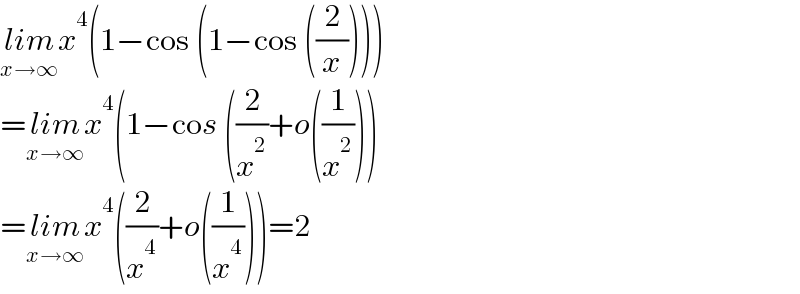
$$\underset{{x}\rightarrow\infty} {{lim}x}^{\mathrm{4}} \left(\mathrm{1}−\mathrm{cos}\:\left(\mathrm{1}−\mathrm{cos}\:\left(\frac{\mathrm{2}}{{x}}\right)\right)\right) \\ $$$$=\underset{{x}\rightarrow\infty} {{lim}x}^{\mathrm{4}} \left(\mathrm{1}−\mathrm{co}{s}\:\left(\frac{\mathrm{2}}{{x}^{\mathrm{2}} }+{o}\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)\right)\right. \\ $$$$=\underset{{x}\rightarrow\infty} {{lim}x}^{\mathrm{4}} \left(\frac{\mathrm{2}}{{x}^{\mathrm{4}} }+{o}\left(\frac{\mathrm{1}}{{x}^{\mathrm{4}} }\right)\right)=\mathrm{2} \\ $$
Answered by cortano1 last updated on 13/Jan/23
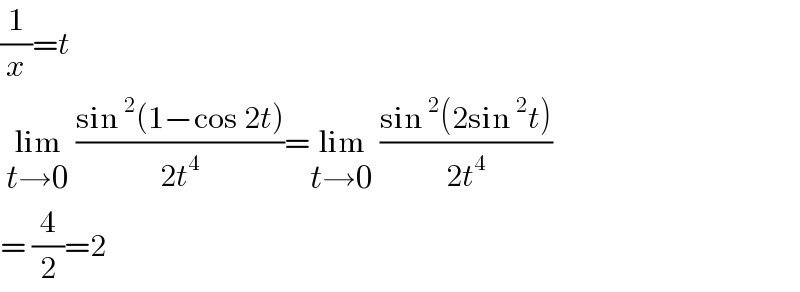
$$\frac{\mathrm{1}}{{x}}={t} \\ $$$$\:\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:^{\mathrm{2}} \left(\mathrm{1}−\mathrm{cos}\:\mathrm{2}{t}\right)}{\mathrm{2}{t}^{\mathrm{4}} }=\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:^{\mathrm{2}} \left(\mathrm{2sin}\:^{\mathrm{2}} {t}\right)}{\mathrm{2}{t}^{\mathrm{4}} } \\ $$$$=\:\frac{\mathrm{4}}{\mathrm{2}}=\mathrm{2} \\ $$
