Question Number 174258 by blackmamba last updated on 28/Jul/22
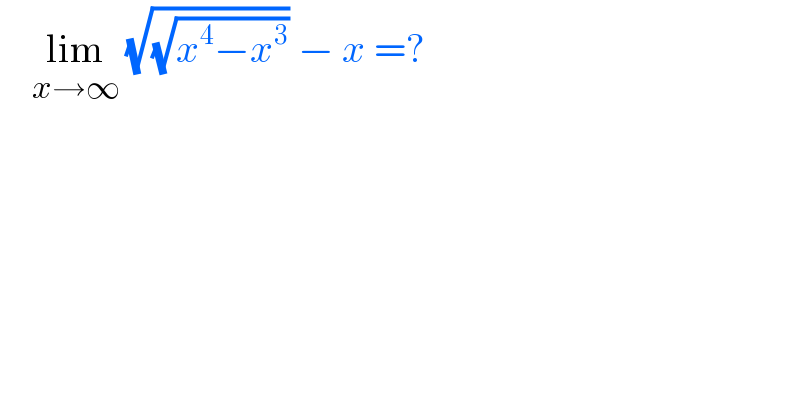
$$\:\:\:\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\sqrt{\sqrt{{x}^{\mathrm{4}} −{x}^{\mathrm{3}} }}\:−\:{x}\:=? \\ $$
Answered by cortano1 last updated on 28/Jul/22
![= lim_(x→∞) (((√(x^4 −x^3 ))−x^2 )/( (√(√(x^4 −x^3 ))) +x)) = lim_(x→∞) ((x^2 ((√(1−(1/x)))−1))/( (√(x^2 (√(1−(1/x)))))+x)) = lim_(x→∞) ((x ((√(1−(1/x)))−1))/( (√(√(1−(1/x)))) +1)) = lim_(x→∞) (((√(1−(1/x)))−1)/((1/x)[(√(√(1−(1/x))))+1])) [ (1/x) = t ∧ t→0 ] = lim_(t→0) (((√(1−t))−1)/(t[(√(√(1−t)))+1 ])) = (1/2) ×lim_(t→0) ((−t)/(t [(√(1−t)) +1 ])) = −(1/4)](https://www.tinkutara.com/question/Q174259.png)
$$\:\:=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\sqrt{{x}^{\mathrm{4}} −{x}^{\mathrm{3}} }−{x}^{\mathrm{2}} }{\:\sqrt{\sqrt{{x}^{\mathrm{4}} −{x}^{\mathrm{3}} }}\:+{x}} \\ $$$$\:=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{{x}^{\mathrm{2}} \left(\sqrt{\mathrm{1}−\frac{\mathrm{1}}{{x}}}−\mathrm{1}\right)}{\:\sqrt{{x}^{\mathrm{2}} \sqrt{\mathrm{1}−\frac{\mathrm{1}}{{x}}}}+{x}} \\ $$$$\:=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{{x}\:\left(\sqrt{\mathrm{1}−\frac{\mathrm{1}}{{x}}}−\mathrm{1}\right)}{\:\sqrt{\sqrt{\mathrm{1}−\frac{\mathrm{1}}{{x}}}}\:+\mathrm{1}} \\ $$$$=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{1}−\frac{\mathrm{1}}{{x}}}−\mathrm{1}}{\frac{\mathrm{1}}{{x}}\left[\sqrt{\sqrt{\mathrm{1}−\frac{\mathrm{1}}{{x}}}}+\mathrm{1}\right]} \\ $$$$\:\left[\:\frac{\mathrm{1}}{{x}}\:=\:{t}\:\wedge\:{t}\rightarrow\mathrm{0}\:\right] \\ $$$$=\:\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{1}−{t}}−\mathrm{1}}{{t}\left[\sqrt{\sqrt{\mathrm{1}−{t}}}+\mathrm{1}\:\right]} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}}\:×\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−{t}}{{t}\:\left[\sqrt{\mathrm{1}−{t}}\:+\mathrm{1}\:\right]} \\ $$$$=\:−\frac{\mathrm{1}}{\mathrm{4}} \\ $$
