Menu Close

lim-x-x-5-1-x-1-

Tinku Tara 0 Comments
Pin




Question Number 113438 by bemath last updated on 13/Sep/20
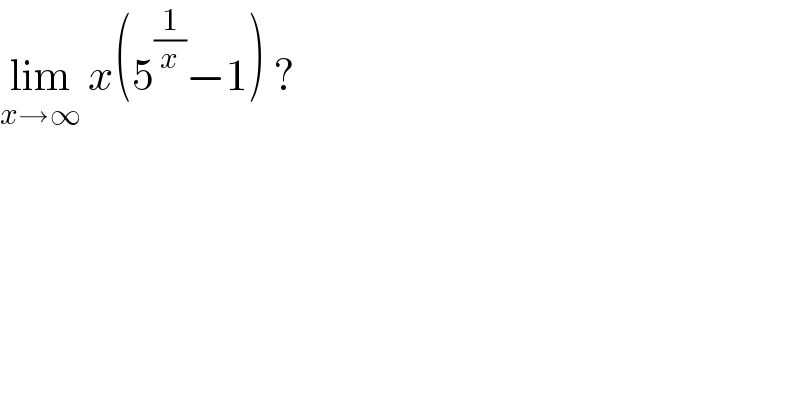
lim_(x→∞) x(5^(1/x) −1) ?
limx→∞x(51x−1)?
Answered by bemath last updated on 13/Sep/20
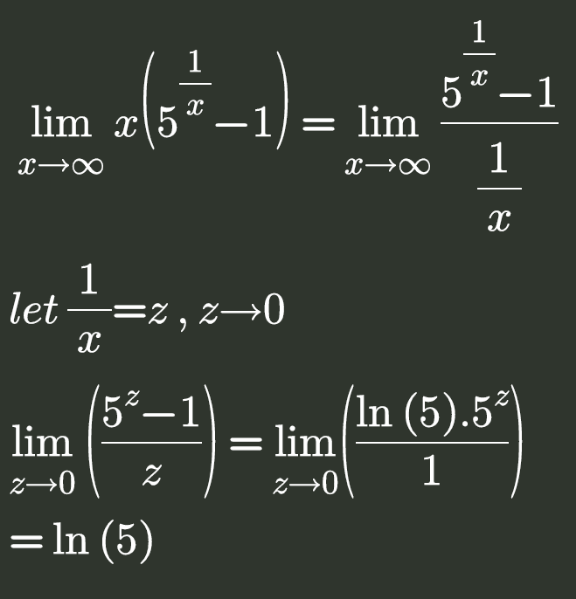
Answered by JDamian last updated on 13/Sep/20
5^(1/x) =e^((ln(5))/x) =1+ (((ln(5))/x)/(1!)) + (((((ln(5))/x))^2 )/(2!)) + (((((ln(5))/x))^3 )/(3!)) + ∙∙∙ lim_(x→∞) x(5^(1/x) −1)= lim_(x→∞) (((ln(5))/(1!)) + ((([ln(5)]^2 )/x)/(2!)) + ((([ln(5)]^3 )/x^2 )/(3!)) + ∙∙∙) = ln(5).
51x=eln(5)x=1+ln(5)x1!+(ln(5)x)22!+(ln(5)x)33!+⋅⋅⋅limx→∞x(51x−1)=limx→∞(ln(5)1!+[ln(5)]2x2!+[ln(5)]3x23!+⋅⋅⋅)=ln(5).

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *