Question Number 149317 by tabata last updated on 04/Aug/21
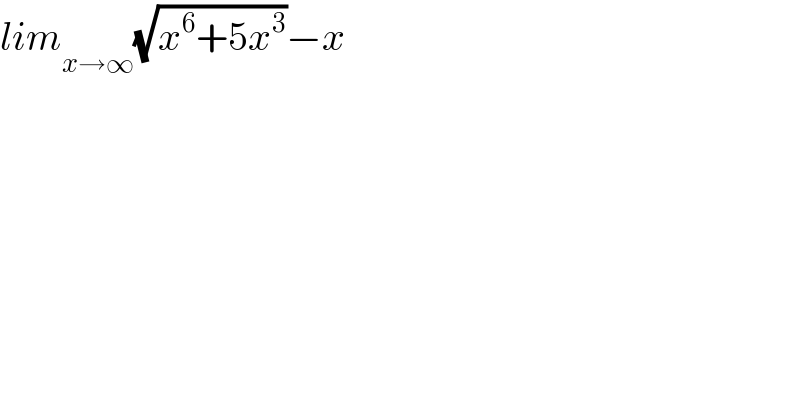
$${lim}_{{x}\rightarrow\infty} \sqrt{{x}^{\mathrm{6}} +\mathrm{5}{x}^{\mathrm{3}} }−{x} \\ $$
Answered by EDWIN88 last updated on 04/Aug/21
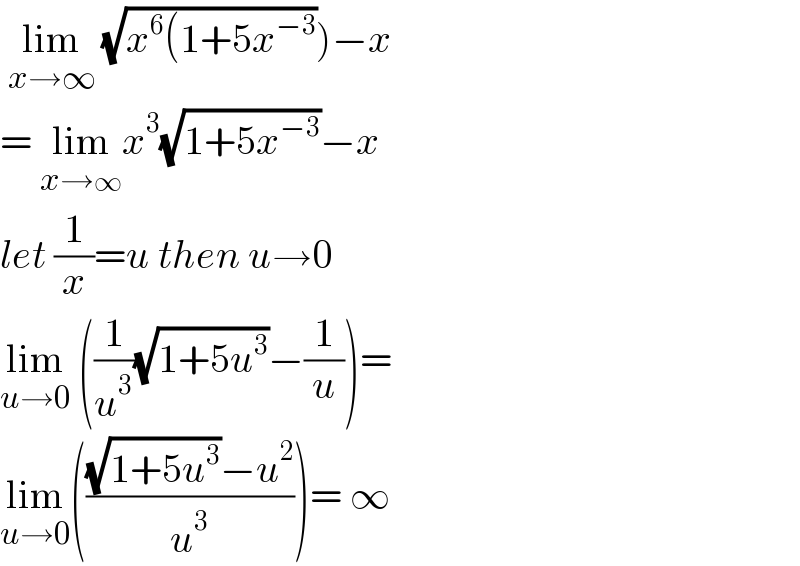
$$\left.\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\sqrt{{x}^{\mathrm{6}} \left(\mathrm{1}+\mathrm{5}{x}^{−\mathrm{3}} \right.}\right)−{x} \\ $$$$=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}{x}^{\mathrm{3}} \sqrt{\mathrm{1}+\mathrm{5}{x}^{−\mathrm{3}} }−{x} \\ $$$${let}\:\frac{\mathrm{1}}{{x}}={u}\:{then}\:{u}\rightarrow\mathrm{0} \\ $$$$\underset{{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\mathrm{1}}{{u}^{\mathrm{3}} }\sqrt{\mathrm{1}+\mathrm{5}{u}^{\mathrm{3}} }−\frac{\mathrm{1}}{{u}}\right)= \\ $$$$\underset{{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\sqrt{\mathrm{1}+\mathrm{5}{u}^{\mathrm{3}} }−{u}^{\mathrm{2}} }{{u}^{\mathrm{3}} }\right)=\:\infty\: \\ $$
Commented by EDWIN88 last updated on 04/Aug/21

$${yes} \\ $$
Commented by JDamian last updated on 04/Aug/21
in the second line, that 0 is actually an infinity
Answered by mathmax by abdo last updated on 04/Aug/21
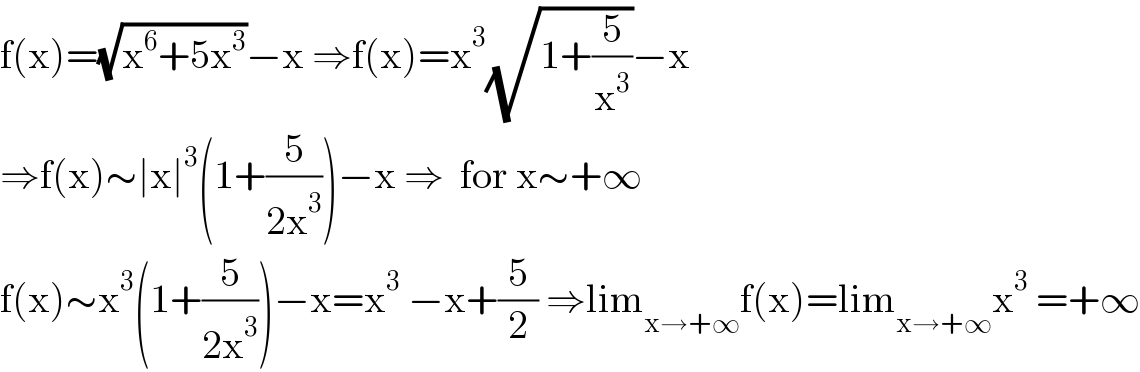
$$\mathrm{f}\left(\mathrm{x}\right)=\sqrt{\mathrm{x}^{\mathrm{6}} +\mathrm{5x}^{\mathrm{3}} }−\mathrm{x}\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\mathrm{x}^{\mathrm{3}} \sqrt{\mathrm{1}+\frac{\mathrm{5}}{\mathrm{x}^{\mathrm{3}} }}−\mathrm{x} \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\sim\mid\mathrm{x}\mid^{\mathrm{3}} \left(\mathrm{1}+\frac{\mathrm{5}}{\mathrm{2x}^{\mathrm{3}} }\right)−\mathrm{x}\:\Rightarrow\:\:\mathrm{for}\:\mathrm{x}\sim+\infty \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\sim\mathrm{x}^{\mathrm{3}} \left(\mathrm{1}+\frac{\mathrm{5}}{\mathrm{2x}^{\mathrm{3}} }\right)−\mathrm{x}=\mathrm{x}^{\mathrm{3}} \:−\mathrm{x}+\frac{\mathrm{5}}{\mathrm{2}}\:\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \mathrm{f}\left(\mathrm{x}\right)=\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \mathrm{x}^{\mathrm{3}} \:=+\infty \\ $$
Commented by mathmax by abdo last updated on 04/Aug/21
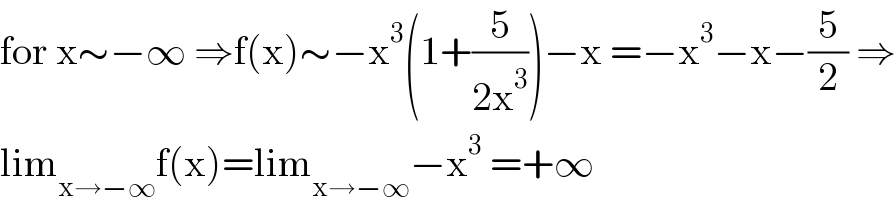
$$\mathrm{for}\:\mathrm{x}\sim−\infty\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\sim−\mathrm{x}^{\mathrm{3}} \left(\mathrm{1}+\frac{\mathrm{5}}{\mathrm{2x}^{\mathrm{3}} }\right)−\mathrm{x}\:=−\mathrm{x}^{\mathrm{3}} −\mathrm{x}−\frac{\mathrm{5}}{\mathrm{2}}\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow−\infty} \mathrm{f}\left(\mathrm{x}\right)=\mathrm{lim}_{\mathrm{x}\rightarrow−\infty} −\mathrm{x}^{\mathrm{3}} \:=+\infty \\ $$
