Menu Close

lim-x-x-7-x-6-1-1-7-x-5-1-x-9-1-9-

Tinku Tara 0 Comments
Pin




Question Number 170766 by cortano1 last updated on 30/May/22
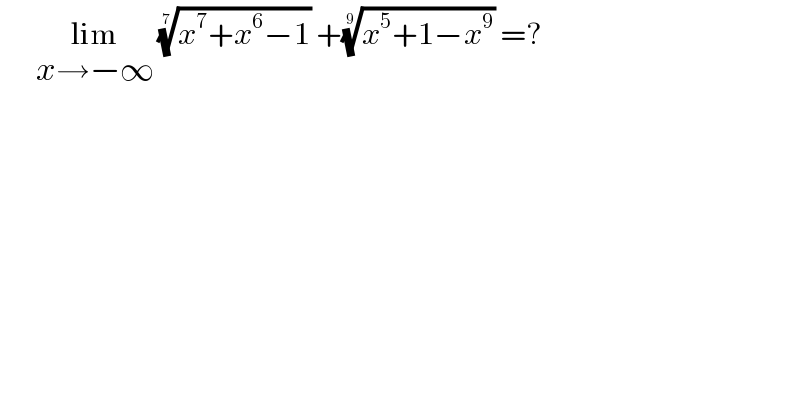
lim_(x→−∞) ((x^7 +x^6 −1))^(1/7) +((x^5 +1−x^9 ))^(1/9) =?
$$\:\:\:\:\:\:\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\:\sqrt[{\mathrm{7}}]{{x}^{\mathrm{7}} +{x}^{\mathrm{6}} −\mathrm{1}}\:+\sqrt[{\mathrm{9}}]{{x}^{\mathrm{5}} +\mathrm{1}−{x}^{\mathrm{9}} }\:=? \\ $$
Answered by aleks041103 last updated on 30/May/22
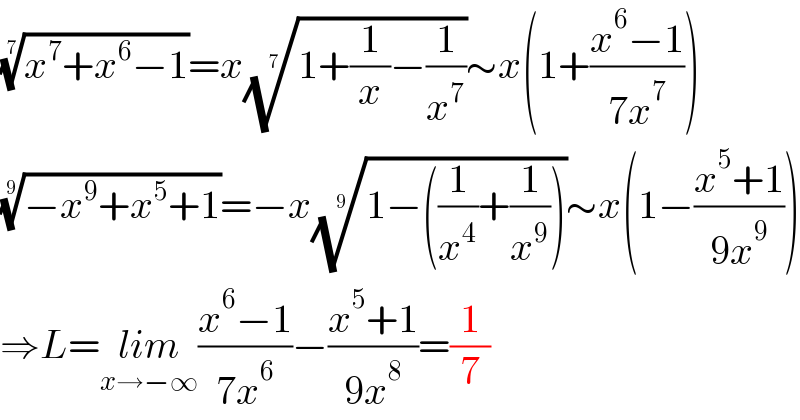
((x^7 +x^6 −1))^(1/7) =x((1+(1/x)−(1/x^7 )))^(1/7) ∼x(1+((x^6 −1)/(7x^7 ))) ((−x^9 +x^5 +1))^(1/9) =−x((1−((1/x^4 )+(1/x^9 ))))^(1/9) ∼x(1−((x^5 +1)/(9x^9 ))) ⇒L=lim_(x→−∞) ((x^6 −1)/(7x^6 ))−((x^5 +1)/(9x^8 ))=(1/7)
$$\sqrt[{\mathrm{7}}]{{x}^{\mathrm{7}} +{x}^{\mathrm{6}} −\mathrm{1}}={x}\sqrt[{\mathrm{7}}]{\mathrm{1}+\frac{\mathrm{1}}{{x}}−\frac{\mathrm{1}}{{x}^{\mathrm{7}} }}\sim{x}\left(\mathrm{1}+\frac{{x}^{\mathrm{6}} −\mathrm{1}}{\mathrm{7}{x}^{\mathrm{7}} }\right) \\ $$$$\sqrt[{\mathrm{9}}]{−{x}^{\mathrm{9}} +{x}^{\mathrm{5}} +\mathrm{1}}=−{x}\sqrt[{\mathrm{9}}]{\mathrm{1}−\left(\frac{\mathrm{1}}{{x}^{\mathrm{4}} }+\frac{\mathrm{1}}{{x}^{\mathrm{9}} }\right)}\sim{x}\left(\mathrm{1}−\frac{{x}^{\mathrm{5}} +\mathrm{1}}{\mathrm{9}{x}^{\mathrm{9}} }\right) \\ $$$$\Rightarrow{L}=\underset{{x}\rightarrow−\infty} {{lim}}\frac{{x}^{\mathrm{6}} −\mathrm{1}}{\mathrm{7}{x}^{\mathrm{6}} }−\frac{{x}^{\mathrm{5}} +\mathrm{1}}{\mathrm{9}{x}^{\mathrm{8}} }=\frac{\mathrm{1}}{\mathrm{7}} \\ $$
Answered by greougoury555 last updated on 31/May/22
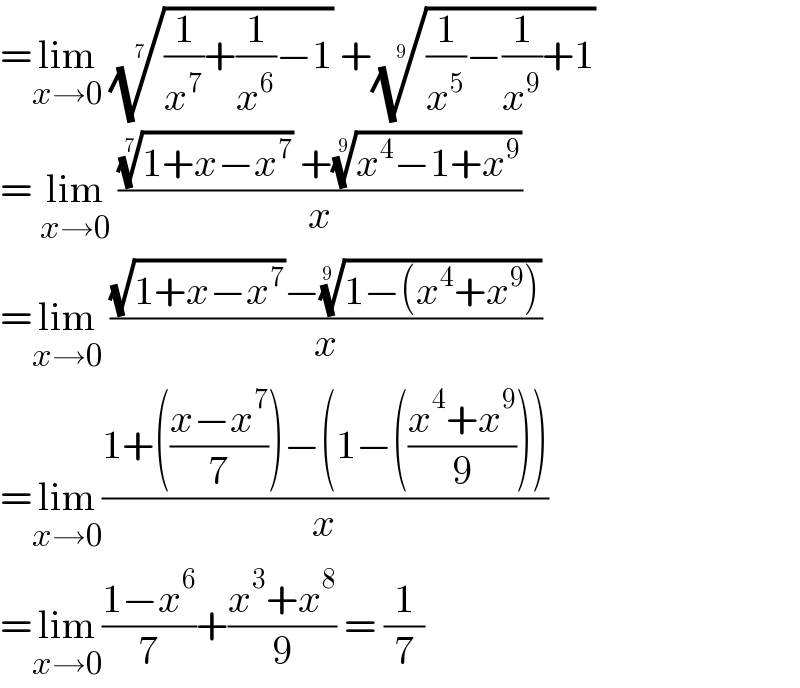
=lim_(x→0) (((1/x^7 )+(1/x^6 )−1))^(1/7) +(((1/x^5 )−(1/x^9 )+1))^(1/9) = lim_(x→0) ((((1+x−x^7 ))^(1/7) +((x^4 −1+x^9 ))^(1/9) )/x) =lim_(x→0) (((√(1+x−x^7 ))−((1−(x^4 +x^9 )))^(1/(9 )) )/x) =lim_(x→0) ((1+(((x−x^7 )/7))−(1−(((x^4 +x^9 )/9))))/x) =lim_(x→0) ((1−x^6 )/7)+((x^3 +x^8 )/9) = (1/7)
$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\sqrt[{\mathrm{7}}]{\frac{\mathrm{1}}{{x}^{\mathrm{7}} }+\frac{\mathrm{1}}{{x}^{\mathrm{6}} }−\mathrm{1}}\:+\sqrt[{\mathrm{9}}]{\frac{\mathrm{1}}{{x}^{\mathrm{5}} }−\frac{\mathrm{1}}{{x}^{\mathrm{9}} }+\mathrm{1}} \\ $$$$=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt[{\mathrm{7}}]{\mathrm{1}+{x}−{x}^{\mathrm{7}} }\:+\sqrt[{\mathrm{9}}]{{x}^{\mathrm{4}} −\mathrm{1}+{x}^{\mathrm{9}} }}{{x}} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{1}+{x}−{x}^{\mathrm{7}} }−\sqrt[{\mathrm{9}\:}]{\mathrm{1}−\left({x}^{\mathrm{4}} +{x}^{\mathrm{9}} \right)}}{{x}} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}+\left(\frac{{x}−{x}^{\mathrm{7}} }{\mathrm{7}}\right)−\left(\mathrm{1}−\left(\frac{{x}^{\mathrm{4}} +{x}^{\mathrm{9}} }{\mathrm{9}}\right)\right)}{{x}} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}−{x}^{\mathrm{6}} }{\mathrm{7}}+\frac{{x}^{\mathrm{3}} +{x}^{\mathrm{8}} }{\mathrm{9}}\:=\:\frac{\mathrm{1}}{\mathrm{7}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *