Question Number 115103 by bobhans last updated on 23/Sep/20

$$\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\sqrt{\left({x}−{a}\right)\left({x}+\mathrm{2}\right)}\:−\sqrt{{x}\left({x}+\mathrm{1}\right)}\:=\:\mathrm{2} \\ $$$${then}\:{a}\:=\:? \\ $$
Commented by Dwaipayan Shikari last updated on 23/Sep/20

$$\underset{{x}\rightarrow\infty} {{l}\mathrm{im}}\frac{\left({x}−{a}\right)\left({x}+\mathrm{2}\right)−{x}^{\mathrm{2}} −{x}}{\:{x}\sqrt{\left(\mathrm{1}−\frac{{a}}{{x}}\right)\left(\mathrm{1}+\frac{\mathrm{2}}{{x}}\right)}+{x}\sqrt{\mathrm{1}+\frac{\mathrm{1}}{{x}}}}=\mathrm{2} \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{{x}^{\mathrm{2}} −{ax}+\mathrm{2}{x}−\mathrm{2}{a}−{x}^{\mathrm{2}} −{x}}{{x}+{x}}=\mathrm{2} \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{−{a}−\mathrm{1}+\mathrm{2}−\frac{\mathrm{2}{a}}{{x}}}{\mathrm{2}}=\mathrm{2} \\ $$$$−{a}+\mathrm{1}=\mathrm{4} \\ $$$${a}=−\mathrm{3} \\ $$$$ \\ $$$${Or} \\ $$$${x}\sqrt{\left(\mathrm{1}−\frac{{a}}{{x}}\right)\left(\mathrm{1}+\frac{\mathrm{2}}{{x}}\right)}\:−{x}\sqrt{\mathrm{1}+\frac{\mathrm{1}}{{x}}}\:=\mathrm{2} \\ $$$${x}\left(\mathrm{1}−\frac{{a}}{\mathrm{2}{x}}+\frac{\mathrm{1}}{{x}}−\frac{{a}}{\mathrm{2}{x}^{\mathrm{2}} }−\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}{x}}\right)=\mathrm{2} \\ $$$$\frac{\mathrm{1}−{a}}{\mathrm{2}}−\frac{{a}}{\mathrm{2}{x}}=\mathrm{2} \\ $$$$\mathrm{1}−{a}=\mathrm{4} \\ $$$${a}=−\mathrm{3} \\ $$
Answered by bemath last updated on 23/Sep/20
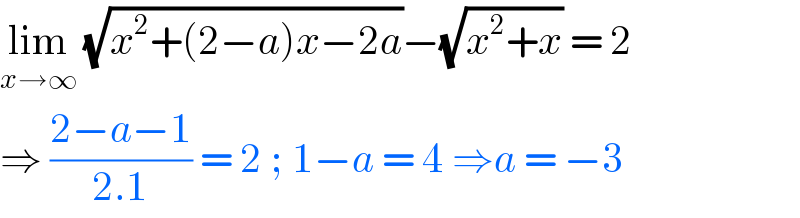
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\sqrt{{x}^{\mathrm{2}} +\left(\mathrm{2}−{a}\right){x}−\mathrm{2}{a}}−\sqrt{{x}^{\mathrm{2}} +{x}}\:=\:\mathrm{2} \\ $$$$\Rightarrow\:\frac{\mathrm{2}−{a}−\mathrm{1}}{\mathrm{2}.\mathrm{1}}\:=\:\mathrm{2}\:;\:\mathrm{1}−{a}\:=\:\mathrm{4}\:\Rightarrow{a}\:=\:−\mathrm{3} \\ $$
Answered by ruwedkabeh last updated on 23/Sep/20
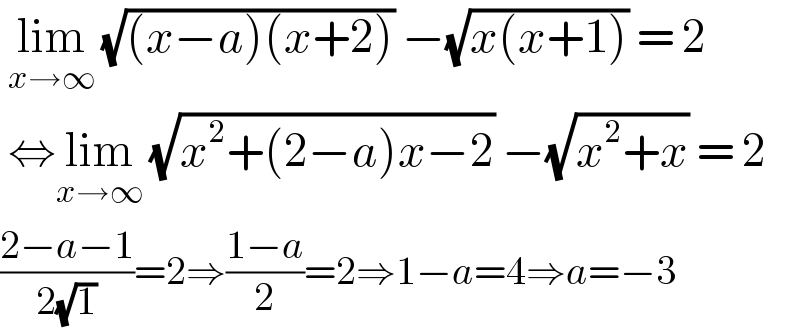
$$\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\sqrt{\left({x}−{a}\right)\left({x}+\mathrm{2}\right)}\:−\sqrt{{x}\left({x}+\mathrm{1}\right)}\:=\:\mathrm{2} \\ $$$$\:\Leftrightarrow\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\sqrt{{x}^{\mathrm{2}} +\left(\mathrm{2}−{a}\right){x}−\mathrm{2}}\:−\sqrt{{x}^{\mathrm{2}} +{x}}\:=\:\mathrm{2} \\ $$$$\frac{\mathrm{2}−{a}−\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{1}}}=\mathrm{2}\Rightarrow\frac{\mathrm{1}−{a}}{\mathrm{2}}=\mathrm{2}\Rightarrow\mathrm{1}−{a}=\mathrm{4}\Rightarrow{a}=−\mathrm{3} \\ $$
Answered by Bird last updated on 24/Sep/20
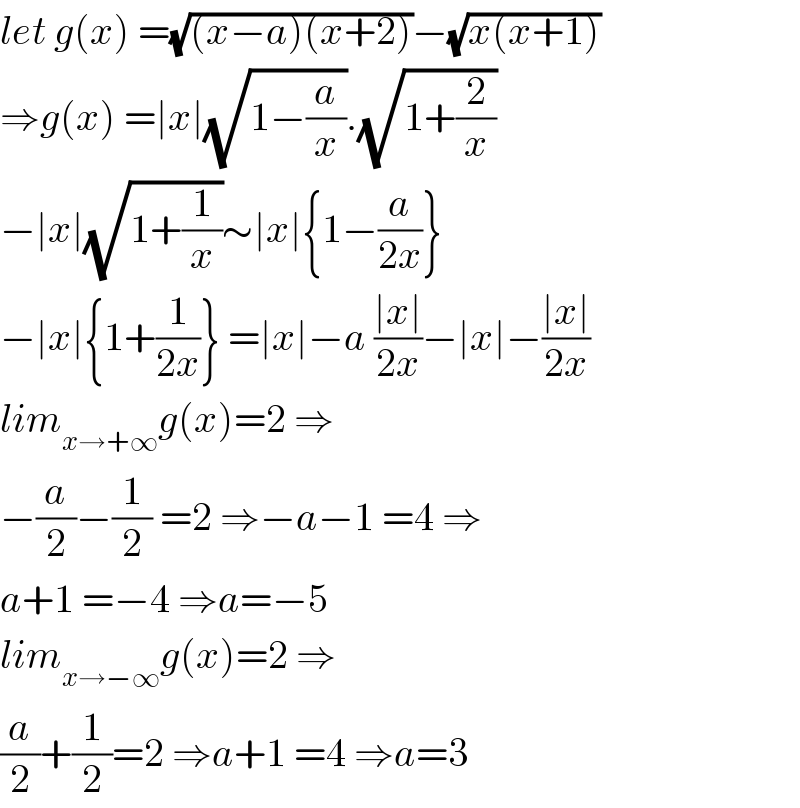
$${let}\:{g}\left({x}\right)\:=\sqrt{\left({x}−{a}\right)\left({x}+\mathrm{2}\right)}−\sqrt{{x}\left({x}+\mathrm{1}\right)} \\ $$$$\Rightarrow{g}\left({x}\right)\:=\mid{x}\mid\sqrt{\mathrm{1}−\frac{{a}}{{x}}}.\sqrt{\mathrm{1}+\frac{\mathrm{2}}{{x}}} \\ $$$$−\mid{x}\mid\sqrt{\mathrm{1}+\frac{\mathrm{1}}{{x}}}\sim\mid{x}\mid\left\{\mathrm{1}−\frac{{a}}{\mathrm{2}{x}}\right\} \\ $$$$−\mid{x}\mid\left\{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}{x}}\right\}\:=\mid{x}\mid−{a}\:\frac{\mid{x}\mid}{\mathrm{2}{x}}−\mid{x}\mid−\frac{\mid{x}\mid}{\mathrm{2}{x}} \\ $$$${lim}_{{x}\rightarrow+\infty} {g}\left({x}\right)=\mathrm{2}\:\Rightarrow \\ $$$$−\frac{{a}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\:=\mathrm{2}\:\Rightarrow−{a}−\mathrm{1}\:=\mathrm{4}\:\Rightarrow \\ $$$${a}+\mathrm{1}\:=−\mathrm{4}\:\Rightarrow{a}=−\mathrm{5} \\ $$$${lim}_{{x}\rightarrow−\infty} {g}\left({x}\right)=\mathrm{2}\:\Rightarrow \\ $$$$\frac{{a}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{2}\:\Rightarrow{a}+\mathrm{1}\:=\mathrm{4}\:\Rightarrow{a}=\mathrm{3} \\ $$
Commented by bemath last updated on 24/Sep/20
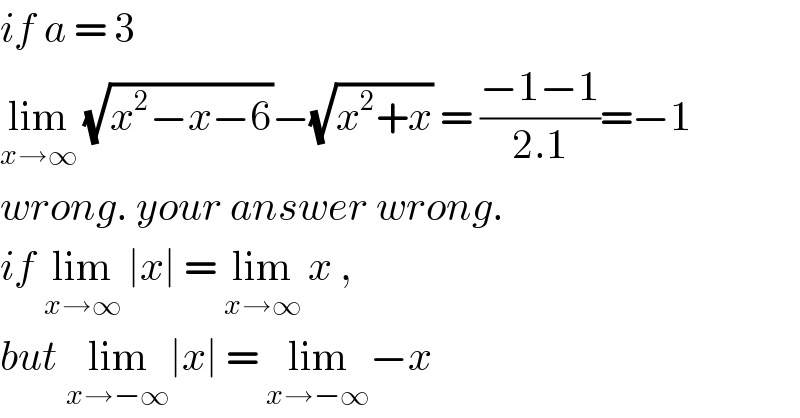
$${if}\:{a}\:=\:\mathrm{3}\: \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\sqrt{{x}^{\mathrm{2}} −{x}−\mathrm{6}}−\sqrt{{x}^{\mathrm{2}} +{x}}\:=\:\frac{−\mathrm{1}−\mathrm{1}}{\mathrm{2}.\mathrm{1}}=−\mathrm{1} \\ $$$${wrong}.\:{your}\:{answer}\:{wrong}. \\ $$$${if}\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\mid{x}\mid\:=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:{x}\:,\: \\ $$$${but}\:\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\mid{x}\mid\:=\:\underset{{x}\rightarrow−\infty} {\mathrm{lim}}−{x} \\ $$
