Question Number 111442 by bobhans last updated on 03/Sep/20
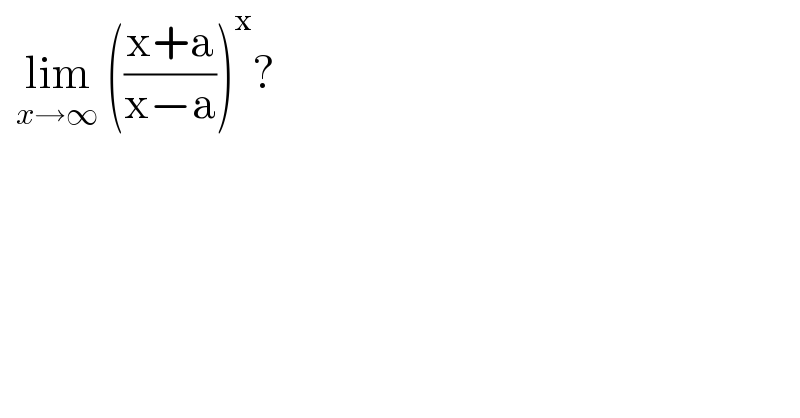
$$\:\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left(\frac{\mathrm{x}+\mathrm{a}}{\mathrm{x}−\mathrm{a}}\right)^{\mathrm{x}} ? \\ $$
Answered by bemath last updated on 03/Sep/20
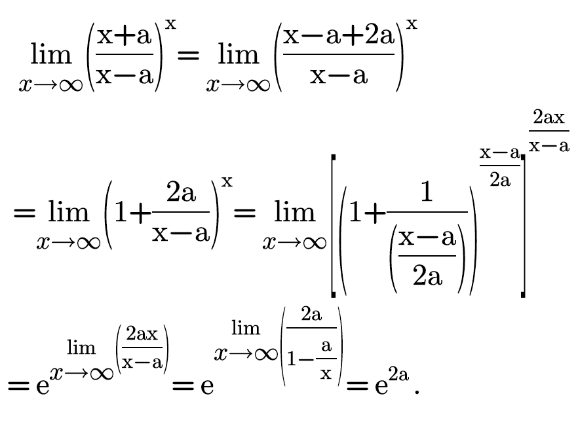
Answered by ajfour last updated on 03/Sep/20
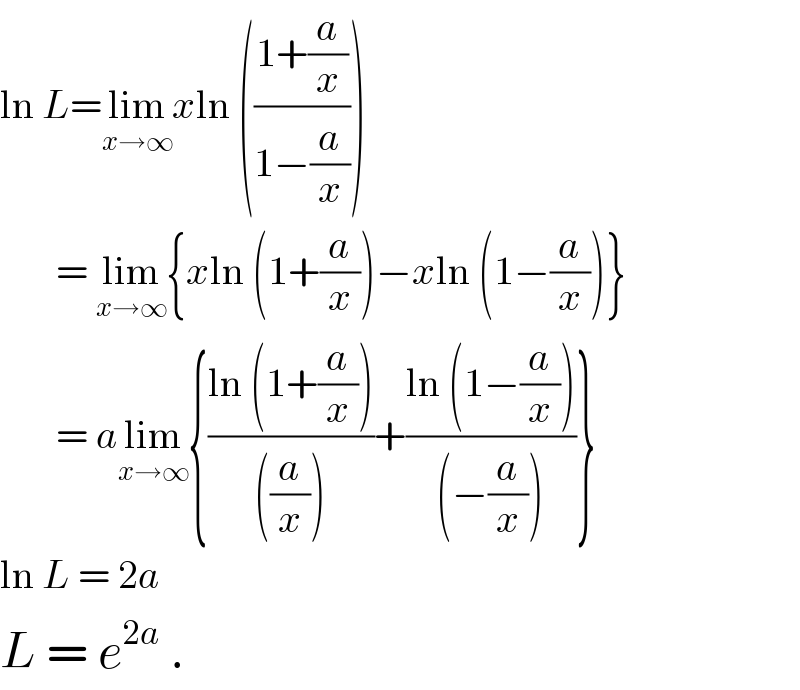
$$\mathrm{ln}\:{L}=\underset{{x}\rightarrow\infty} {\mathrm{lim}}{x}\mathrm{ln}\:\left(\frac{\mathrm{1}+\frac{{a}}{{x}}}{\mathrm{1}−\frac{{a}}{{x}}}\right) \\ $$$$\:\:\:\:\:\:\:=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left\{{x}\mathrm{ln}\:\left(\mathrm{1}+\frac{{a}}{{x}}\right)−{x}\mathrm{ln}\:\left(\mathrm{1}−\frac{{a}}{{x}}\right)\right\} \\ $$$$\:\:\:\:\:\:\:=\:{a}\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left\{\frac{\mathrm{ln}\:\left(\mathrm{1}+\frac{{a}}{{x}}\right)}{\left(\frac{{a}}{{x}}\right)}+\frac{\mathrm{ln}\:\left(\mathrm{1}−\frac{{a}}{{x}}\right)}{\left(−\frac{{a}}{{x}}\right)}\right\} \\ $$$$\mathrm{ln}\:{L}\:=\:\mathrm{2}{a} \\ $$$${L}\:=\:{e}^{\mathrm{2}{a}} \:. \\ $$
Answered by Dwaipayan Shikari last updated on 03/Sep/20
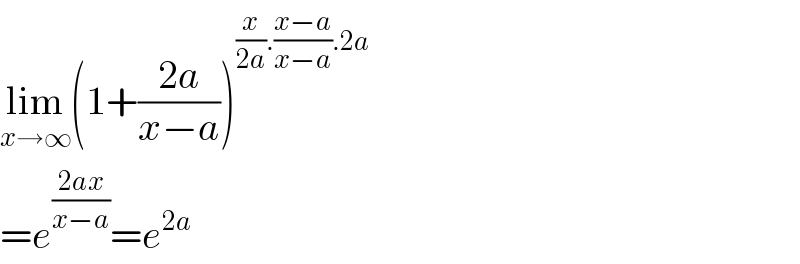
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{1}+\frac{\mathrm{2}{a}}{{x}−{a}}\right)^{\frac{{x}}{\mathrm{2}{a}}.\frac{{x}−{a}}{{x}−{a}}.\mathrm{2}{a}} \\ $$$$={e}^{\frac{\mathrm{2}{ax}}{{x}−{a}}} ={e}^{\mathrm{2}{a}} \\ $$
