Question Number 110260 by bemath last updated on 28/Aug/20
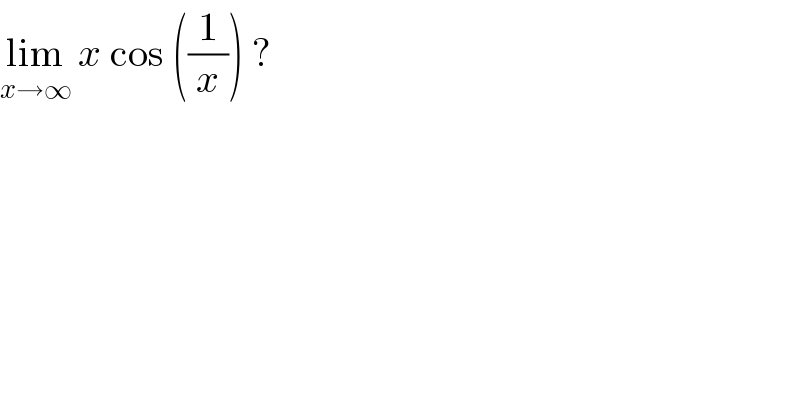
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:{x}\:\mathrm{cos}\:\left(\frac{\mathrm{1}}{{x}}\right)\:? \\ $$
Answered by john santu last updated on 28/Aug/20
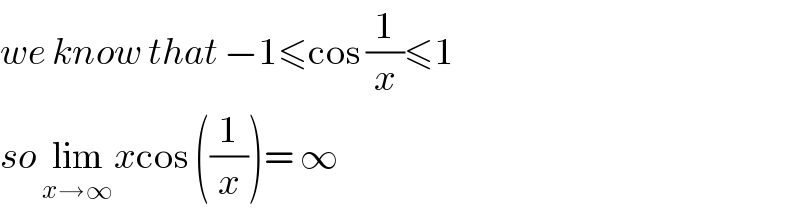
$${we}\:{know}\:{that}\:−\mathrm{1}\leqslant\mathrm{cos}\:\frac{\mathrm{1}}{{x}}\leqslant\mathrm{1}\: \\ $$$${so}\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}{x}\mathrm{cos}\:\left(\frac{\mathrm{1}}{{x}}\right)=\:\infty \\ $$
Commented by Her_Majesty last updated on 28/Aug/20
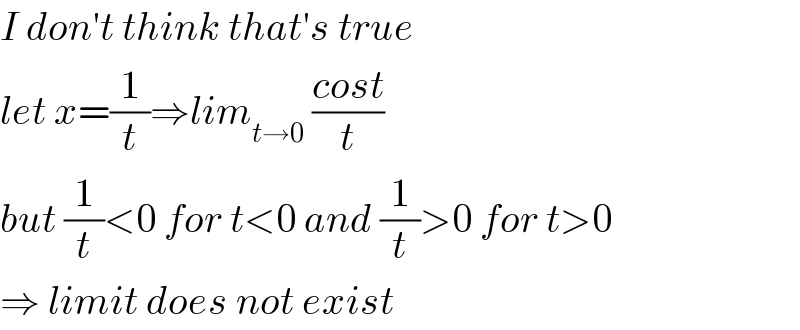
$${I}\:{don}'{t}\:{think}\:{that}'{s}\:{true} \\ $$$${let}\:{x}=\frac{\mathrm{1}}{{t}}\Rightarrow{lim}_{{t}\rightarrow\mathrm{0}} \:\frac{{cost}}{{t}} \\ $$$${but}\:\frac{\mathrm{1}}{{t}}<\mathrm{0}\:{for}\:{t}<\mathrm{0}\:{and}\:\frac{\mathrm{1}}{{t}}>\mathrm{0}\:{for}\:{t}>\mathrm{0} \\ $$$$\Rightarrow\:{limit}\:{does}\:{not}\:{exist} \\ $$
Commented by john santu last updated on 28/Aug/20

$${no} \\ $$
Commented by john santu last updated on 28/Aug/20
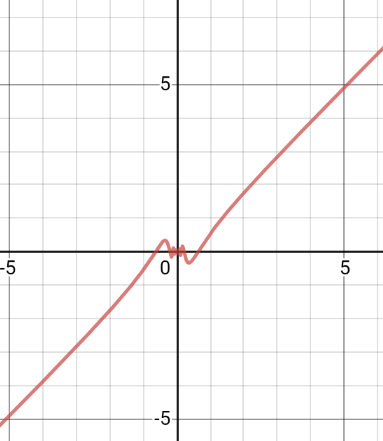
Commented by john santu last updated on 28/Aug/20
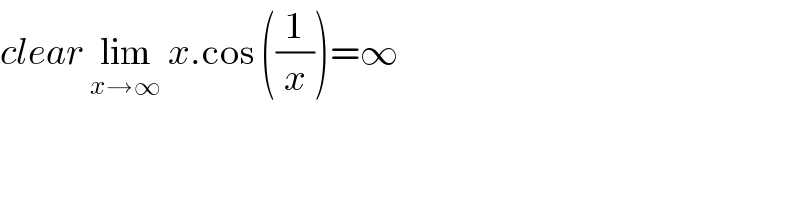
$${clear}\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:{x}.\mathrm{cos}\:\left(\frac{\mathrm{1}}{{x}}\right)=\infty \\ $$
Commented by Her_Majesty last updated on 28/Aug/20
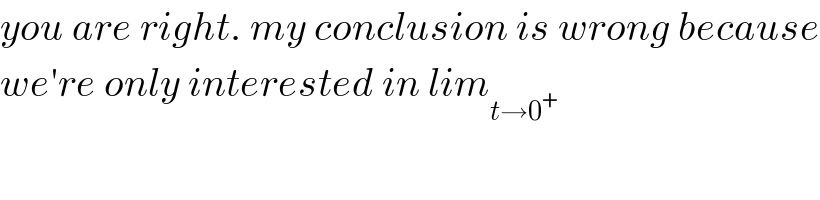
$${you}\:{are}\:{right}.\:{my}\:{conclusion}\:{is}\:{wrong}\:{because} \\ $$$${we}'{re}\:{only}\:{interested}\:{in}\:{lim}_{{t}\rightarrow\mathrm{0}^{+} } \\ $$
