Question Number 27830 by çhëý böý last updated on 15/Jan/18

$$\underset{{x}\rightarrow\propto} {\mathrm{lim}}\:\left({x}−\mathrm{ln}{x}\right) \\ $$
Commented by abdo imad last updated on 15/Jan/18
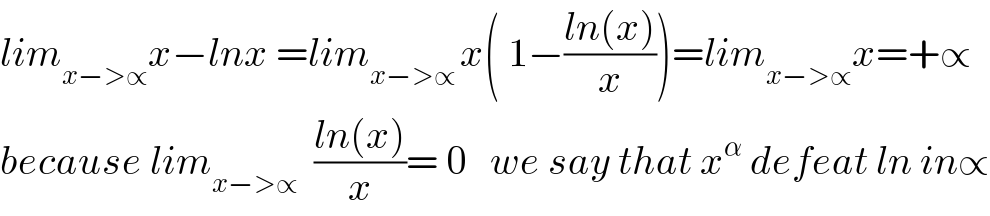
$${lim}_{{x}−>\propto} {x}−{lnx}\:={lim}_{{x}−>\propto\:} {x}\left(\:\mathrm{1}−\frac{{ln}\left({x}\right)}{{x}}\right)={lim}_{{x}−>\propto} {x}=+\propto \\ $$$${because}\:{lim}_{{x}−>\propto} \:\:\frac{{ln}\left({x}\right)}{{x}}=\:\mathrm{0}\:\:\:{we}\:{say}\:{that}\:{x}^{\alpha} \:{defeat}\:{ln}\:{in}\propto \\ $$
