Question Number 28084 by tawa tawa last updated on 20/Jan/18
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\:\left(\mathrm{x}\:−\:\mathrm{log}_{\mathrm{e}} \mathrm{x}\right) \\ $$
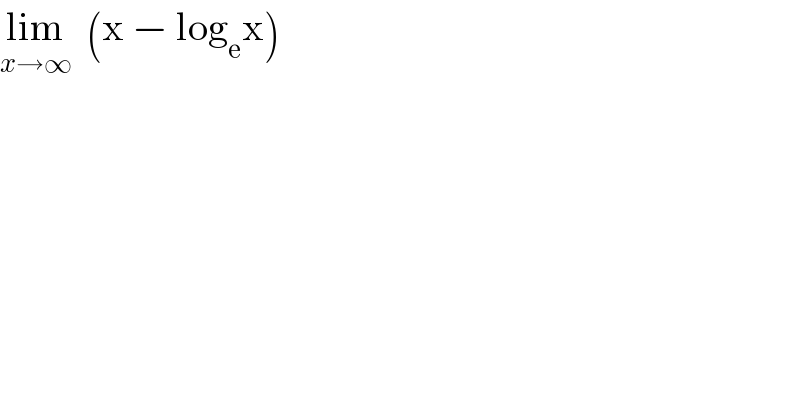
Commented by çhëý böý last updated on 20/Jan/18
$$\underset{{x}\rightarrow\propto} {\mathrm{lim}}\:\:\left({x}−{lnx}\right) \\ $$$$\underset{{x}\rightarrow\propto\:} {\mathrm{lim}}\:\:\left({lne}^{{x}} −{lnx}\right) \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\:{ln}\:\left(\frac{{e}^{{x}} }{{lnx}}\right) \\ $$$${l}'{hopital} \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\:\frac{{e}^{{x}} }{\frac{\mathrm{1}}{{x}}}=\:\frac{{e}^{\infty} }{\mathrm{0}}={DNE} \\ $$
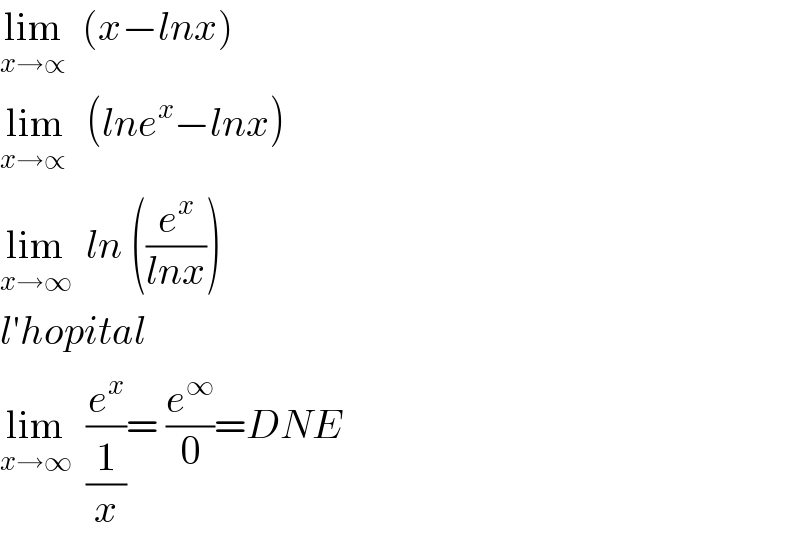
Commented by tawa tawa last updated on 20/Jan/18
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by abdo imad last updated on 20/Jan/18
![we know that D_(lnx) =]0,+∞[ so lim_(x→+∞^ ) ^ (x−lnx)=lim_(x→+∞) x(1− ((lnx)/x))=lim_(x→+∞) x =+∞ because lim_(x→+∞^ ) ((lnx)/x)=0 .](https://www.tinkutara.com/question/Q28118.png)
$$\left.{we}\:{know}\:{that}\:\:{D}_{{lnx}} =\right]\mathrm{0},+\infty\left[\:\:\:{so}\right. \\ $$$${lim}_{{x}\rightarrow+\infty^{} } ^{} \left({x}−{lnx}\right)={lim}_{{x}\rightarrow+\infty} {x}\left(\mathrm{1}−\:\frac{{lnx}}{{x}}\right)={lim}_{{x}\rightarrow+\infty} {x} \\ $$$$=+\infty\:\:{because}\:\:{lim}_{{x}\rightarrow+\infty^{} } \frac{{lnx}}{{x}}=\mathrm{0}\:. \\ $$
Commented by abdo imad last updated on 20/Jan/18
$${ln}\left(\frac{{e}^{{x}} }{{lnx}}\right)=\:{x}−{ln}\left({lnx}\right)\neq\:{ln}\left({e}^{{x}} \right)\:−{lnx}\:{you}\:{have}\:{commited}\:{a} \\ $$$${error}\:{sir}\:. \\ $$
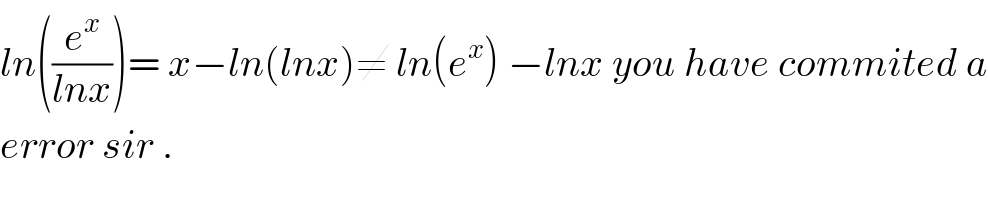
Commented by çhëý böý last updated on 20/Jan/18
$${yeah}\:{i}\:{made}\:{mistake}\:{it}\:{should}\:{be} \\ $$$${ln}\:\:\frac{\left({e}^{{x}} \right)^{'} }{\left({x}\right)^{'} }=\frac{{e}^{{x}} }{\mathrm{1}}\:={e}^{\infty} =\infty \\ $$$${thank}\:{u}\:{for}\:{d}\:{rectification}\:{sir} \\ $$$$ \\ $$
Commented by tawa tawa last updated on 21/Jan/18
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$