lim-x-x-sin-1-x-x-2-

Question Number 117820 by islam last updated on 13/Oct/20

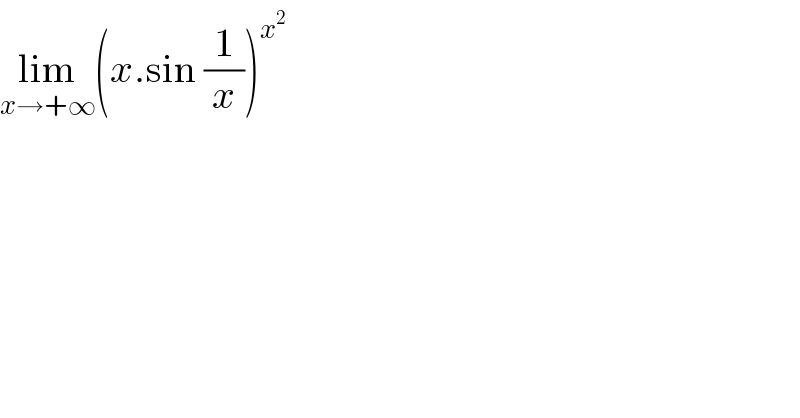
$$\underset{{x}\rightarrow+\infty} {\mathrm{lim}}\left({x}.\mathrm{sin}\:\frac{\mathrm{1}}{{x}}\right)^{{x}^{\mathrm{2}} } \\ $$

Answered by Dwaipayan Shikari last updated on 13/Oct/20

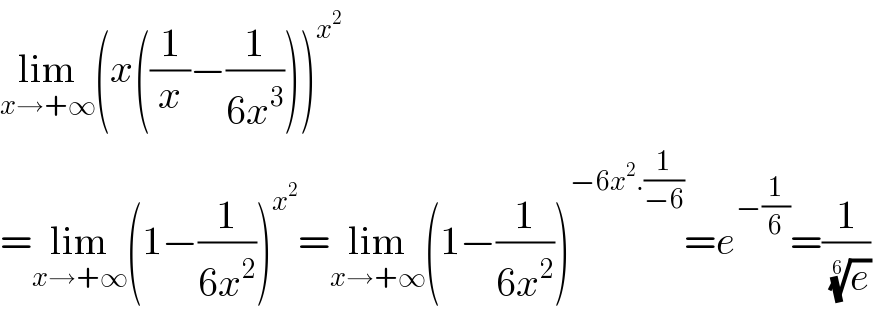
lim_(x→+∞) (x((1/x)−(1/(6x^3 ))))^x^2 =lim_(x→+∞) (1−(1/(6x^2 )))^x^2 =lim_(x→+∞) (1−(1/(6x^2 )))^(−6x^2 .(1/(−6))) =e^(−(1/6)) =(1/( (e)^(1/6) ))

$$\underset{{x}\rightarrow+\infty} {\mathrm{lim}}\left({x}\left(\frac{\mathrm{1}}{{x}}−\frac{\mathrm{1}}{\mathrm{6}{x}^{\mathrm{3}} }\right)\right)^{{x}^{\mathrm{2}} } \\ $$$$=\underset{{x}\rightarrow+\infty} {\mathrm{lim}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{6}{x}^{\mathrm{2}} }\right)^{{x}^{\mathrm{2}} } =\underset{{x}\rightarrow+\infty} {\mathrm{lim}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{6}{x}^{\mathrm{2}} }\right)^{−\mathrm{6}{x}^{\mathrm{2}} .\frac{\mathrm{1}}{−\mathrm{6}}} ={e}^{−\frac{\mathrm{1}}{\mathrm{6}}} =\frac{\mathrm{1}}{\:\sqrt[{\mathrm{6}}]{{e}}} \\ $$

Answered by mathmax by abdo last updated on 13/Oct/20

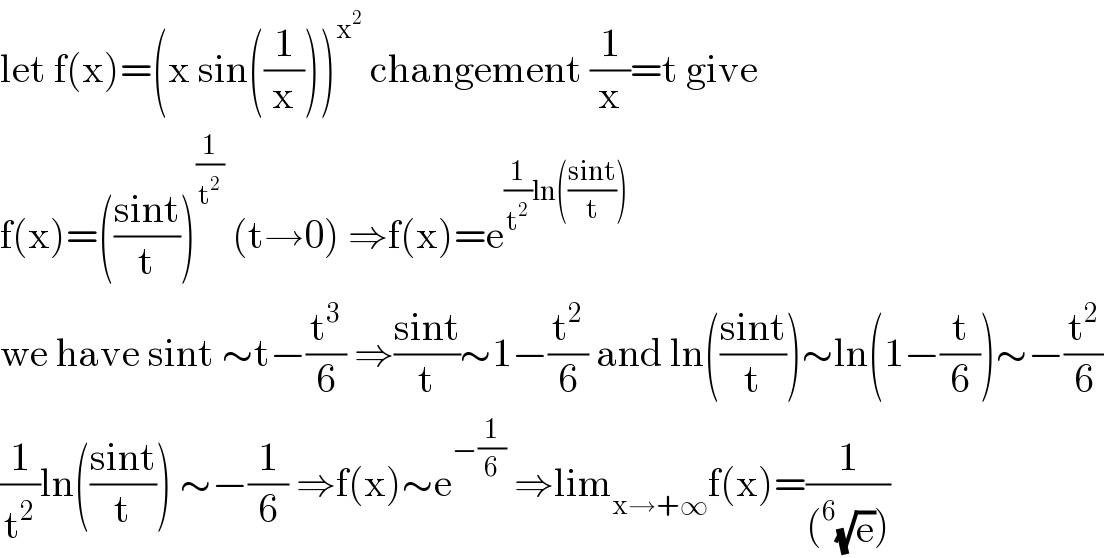
let f(x)=(x sin((1/x)))^x^2 changement (1/x)=t give f(x)=(((sint)/t))^(1/t^2 ) (t→0) ⇒f(x)=e^((1/t^2 )ln(((sint)/t))) we have sint ∼t−(t^3 /6) ⇒((sint)/t)∼1−(t^2 /6) and ln(((sint)/t))∼ln(1−(t/6))∼−(t^2 /6) (1/t^2 )ln(((sint)/t)) ∼−(1/6) ⇒f(x)∼e^(−(1/6)) ⇒lim_(x→+∞) f(x)=(1/((^6 (√e))))

$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)=\left(\mathrm{x}\:\mathrm{sin}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)\right)^{\mathrm{x}^{\mathrm{2}} } \:\mathrm{changement}\:\frac{\mathrm{1}}{\mathrm{x}}=\mathrm{t}\:\mathrm{give} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\left(\frac{\mathrm{sint}}{\mathrm{t}}\right)^{\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }} \:\left(\mathrm{t}\rightarrow\mathrm{0}\right)\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }\mathrm{ln}\left(\frac{\mathrm{sint}}{\mathrm{t}}\right)} \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{sint}\:\sim\mathrm{t}−\frac{\mathrm{t}^{\mathrm{3}} }{\mathrm{6}}\:\Rightarrow\frac{\mathrm{sint}}{\mathrm{t}}\sim\mathrm{1}−\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{6}}\:\mathrm{and}\:\mathrm{ln}\left(\frac{\mathrm{sint}}{\mathrm{t}}\right)\sim\mathrm{ln}\left(\mathrm{1}−\frac{\mathrm{t}}{\mathrm{6}}\right)\sim−\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{6}} \\ $$$$\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }\mathrm{ln}\left(\frac{\mathrm{sint}}{\mathrm{t}}\right)\:\sim−\frac{\mathrm{1}}{\mathrm{6}}\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\sim\mathrm{e}^{−\frac{\mathrm{1}}{\mathrm{6}}} \:\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\left(^{\mathrm{6}} \sqrt{\mathrm{e}}\right)} \\ $$

Answered by john santu last updated on 14/Oct/20

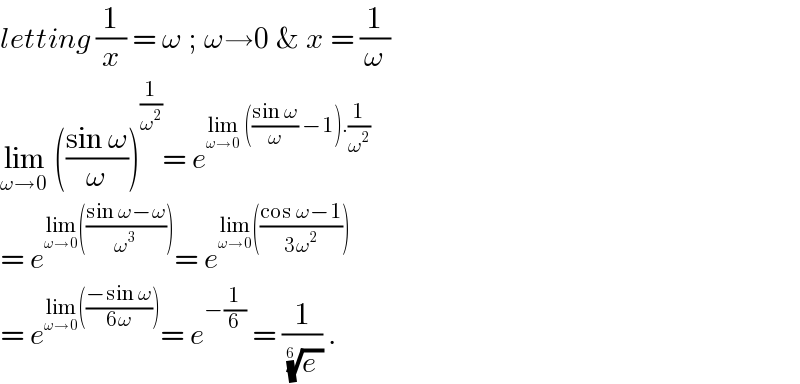
letting (1/x) = ω ; ω→0 & x = (1/ω) lim_(ω→0) (((sin ω)/ω))^(1/ω^2 ) = e^(lim_(ω→0) (((sin ω)/ω) −1).(1/ω^2 )) = e^(lim_(ω→0) (((sin ω−ω)/ω^3 ))) = e^(lim_(ω→0) (((cos ω−1)/(3ω^2 )))) = e^(lim_(ω→0) (((−sin ω)/(6ω)))) = e^(−(1/6)) = (1/( ((e ))^(1/(6 )) )) .

$${letting}\:\frac{\mathrm{1}}{{x}}\:=\:\omega\:;\:\omega\rightarrow\mathrm{0}\:\&\:{x}\:=\:\frac{\mathrm{1}}{\omega} \\ $$$$\underset{\omega\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\mathrm{sin}\:\omega}{\omega}\right)^{\frac{\mathrm{1}}{\omega^{\mathrm{2}} }} =\:{e}^{\underset{\omega\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\mathrm{sin}\:\omega}{\omega}\:−\mathrm{1}\right).\frac{\mathrm{1}}{\omega^{\mathrm{2}} }} \\ $$$$=\:{e}^{\underset{\omega\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{sin}\:\omega−\omega}{\omega^{\mathrm{3}} }\right)} =\:{e}^{\underset{\omega\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{cos}\:\omega−\mathrm{1}}{\mathrm{3}\omega^{\mathrm{2}} }\right)} \\ $$$$=\:{e}^{\underset{\omega\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{−\mathrm{sin}\:\omega}{\mathrm{6}\omega}\right)} =\:{e}^{−\frac{\mathrm{1}}{\mathrm{6}}} \:=\:\frac{\mathrm{1}}{\:\sqrt[{\mathrm{6}\:}]{{e}\:}}\:. \\ $$

Facebook Tweet Pin

lim-x-x-sin-1-x-x-2-

Leave a Reply Cancel reply