lim-x-x-x-1-9x-2-x-3-

Question Number 123349 by bemath last updated on 25/Nov/20

$$\:\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left[\:{x}\:\sqrt{\frac{{x}−\mathrm{1}}{\mathrm{9}{x}+\mathrm{2}}}\:−\frac{{x}}{\mathrm{3}}\:\right]? \\ $$

Answered by liberty last updated on 25/Nov/20

lim_(x→∞) x [(√((x−1)/(9x+2))) − (1/3) ]= lim_(x→∞) ((x (3(√(x−1)) −(√(9x+2))))/( 3(√(9x+2)))) = lim_(x→∞) ((x((√(9x−9))−(√(9x+2))))/( (√(9x+2)))) = lim_(x→∞) ((x (9x−9−9x−2))/( 3(√(9x+2)) ((√(9x−9))+(√(9x+2))))) = lim_(x→∞) ((−11x)/(3x (√(9+(2/x))) ((√(9−(9/x)))+(√(9+(2/x))))))= ((−11)/(9(3+3))) = −((11)/(54))

$$\:\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:{x}\:\left[\sqrt{\frac{{x}−\mathrm{1}}{\mathrm{9}{x}+\mathrm{2}}}\:−\:\frac{\mathrm{1}}{\mathrm{3}}\:\right]= \\ $$$$\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{{x}\:\left(\mathrm{3}\sqrt{{x}−\mathrm{1}}\:−\sqrt{\mathrm{9}{x}+\mathrm{2}}\right)}{\:\mathrm{3}\sqrt{\mathrm{9}{x}+\mathrm{2}}}\:= \\ $$$$\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{{x}\left(\sqrt{\mathrm{9}{x}−\mathrm{9}}−\sqrt{\mathrm{9}{x}+\mathrm{2}}\right)}{\:\sqrt{\mathrm{9}{x}+\mathrm{2}}}\:= \\ $$$$\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{{x}\:\left(\mathrm{9}{x}−\mathrm{9}−\mathrm{9}{x}−\mathrm{2}\right)}{\:\mathrm{3}\sqrt{\mathrm{9}{x}+\mathrm{2}}\:\left(\sqrt{\mathrm{9}{x}−\mathrm{9}}+\sqrt{\mathrm{9}{x}+\mathrm{2}}\right)}\:= \\ $$$$\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{−\mathrm{11}{x}}{\mathrm{3}{x}\:\sqrt{\mathrm{9}+\frac{\mathrm{2}}{{x}}}\:\left(\sqrt{\mathrm{9}−\frac{\mathrm{9}}{{x}}}+\sqrt{\mathrm{9}+\frac{\mathrm{2}}{{x}}}\right)}= \\ $$$$\:\:\frac{−\mathrm{11}}{\mathrm{9}\left(\mathrm{3}+\mathrm{3}\right)}\:=\:−\frac{\mathrm{11}}{\mathrm{54}} \\ $$

Commented by bemath last updated on 25/Nov/20

$${typo}\:{it}\:{should}\:{be}\:−\frac{\mathrm{11}}{\mathrm{54}} \\ $$

Commented by liberty last updated on 25/Nov/20

$${yes}. \\ $$

Answered by Bird last updated on 25/Nov/20

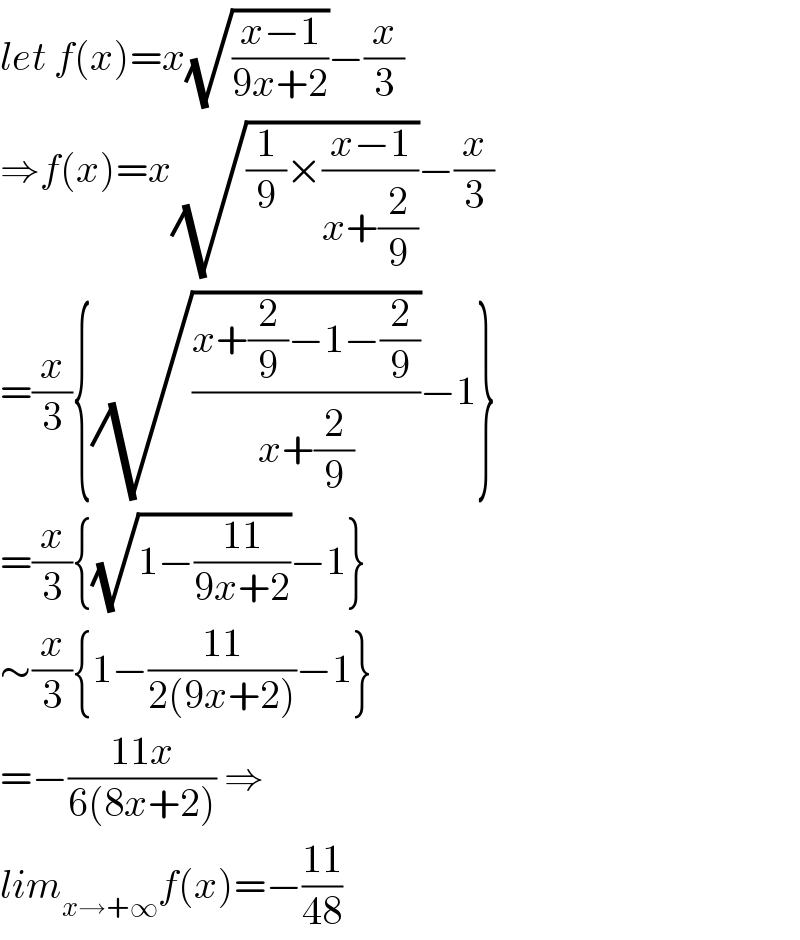
let f(x)=x(√((x−1)/(9x+2)))−(x/3) ⇒f(x)=x(√((1/9)×((x−1)/(x+(2/9)))))−(x/3) =(x/3){(√((x+(2/9)−1−(2/9))/(x+(2/9))))−1} =(x/3){(√(1−((11)/(9x+2))))−1} ∼(x/3){1−((11)/(2(9x+2)))−1} =−((11x)/(6(8x+2))) ⇒ lim_(x→+∞) f(x)=−((11)/(48))

$${let}\:{f}\left({x}\right)={x}\sqrt{\frac{{x}−\mathrm{1}}{\mathrm{9}{x}+\mathrm{2}}}−\frac{{x}}{\mathrm{3}} \\ $$$$\Rightarrow{f}\left({x}\right)={x}\sqrt{\frac{\mathrm{1}}{\mathrm{9}}×\frac{{x}−\mathrm{1}}{{x}+\frac{\mathrm{2}}{\mathrm{9}}}}−\frac{{x}}{\mathrm{3}} \\ $$$$=\frac{{x}}{\mathrm{3}}\left\{\sqrt{\frac{{x}+\frac{\mathrm{2}}{\mathrm{9}}−\mathrm{1}−\frac{\mathrm{2}}{\mathrm{9}}}{{x}+\frac{\mathrm{2}}{\mathrm{9}}}}−\mathrm{1}\right\} \\ $$$$=\frac{{x}}{\mathrm{3}}\left\{\sqrt{\mathrm{1}−\frac{\mathrm{11}}{\mathrm{9}{x}+\mathrm{2}}}−\mathrm{1}\right\} \\ $$$$\sim\frac{{x}}{\mathrm{3}}\left\{\mathrm{1}−\frac{\mathrm{11}}{\mathrm{2}\left(\mathrm{9}{x}+\mathrm{2}\right)}−\mathrm{1}\right\} \\ $$$$=−\frac{\mathrm{11}{x}}{\mathrm{6}\left(\mathrm{8}{x}+\mathrm{2}\right)}\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow+\infty} {f}\left({x}\right)=−\frac{\mathrm{11}}{\mathrm{48}} \\ $$

Commented by Bird last updated on 25/Nov/20

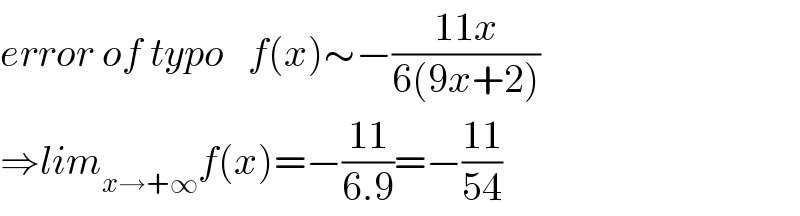
error of typo f(x)∼−((11x)/(6(9x+2))) ⇒lim_(x→+∞) f(x)=−((11)/(6.9))=−((11)/(54))

$${error}\:{of}\:{typo}\:\:\:{f}\left({x}\right)\sim−\frac{\mathrm{11}{x}}{\mathrm{6}\left(\mathrm{9}{x}+\mathrm{2}\right)} \\ $$$$\Rightarrow{lim}_{{x}\rightarrow+\infty} {f}\left({x}\right)=−\frac{\mathrm{11}}{\mathrm{6}.\mathrm{9}}=−\frac{\mathrm{11}}{\mathrm{54}} \\ $$

Facebook Tweet Pin

lim-x-x-x-1-9x-2-x-3-

Leave a Reply Cancel reply