Question Number 129199 by Adel last updated on 13/Jan/21
![lim_(x→∞) [(x^(x+1) /((x+1)^x ))−(((x−1)^x )/x^(x−1) )]=? solve tish pleas](https://www.tinkutara.com/question/Q129199.png)
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left[\frac{\mathrm{x}^{\mathrm{x}+\mathrm{1}} }{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{x}} }−\frac{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{x}} }{\mathrm{x}^{\mathrm{x}−\mathrm{1}} }\right]=? \\ $$$$\mathrm{solve}\:\:\:\mathrm{tish}\:\:\mathrm{pleas} \\ $$
Answered by mr W last updated on 13/Jan/21
![=lim_(x→∞) [(x/((1+(1/x))^x ))−x(1−(1/x))^x ] =lim_(x→∞) (1/((1+(1/x))^x ))×[x−x(1−(1/x^2 ))^x ] =lim_(x→∞) (1/((1+(1/x))^x ))×[x−x(1−(1/x)+(1/(2x^2 ))−(2/(3x^3 ))+o((1/x^4 )))] =lim_(x→∞) (1/((1+(1/x))^x ))×[x−x+1−(1/(2x))+(2/(3x^2 ))−o((1/x^3 ))] =lim_(x→∞) (1/((1+(1/x))^x ))×[1−(1/(2x))+(2/(3x^2 ))−o((1/x^3 ))] =(1/e)](https://www.tinkutara.com/question/Q129203.png)
$$=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left[\frac{{x}}{\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)^{{x}} }−{x}\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right)^{{x}} \right] \\ $$$$=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)^{{x}} }×\left[{x}−{x}\left(\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)^{{x}} \right] \\ $$$$=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)^{{x}} }×\left[{x}−{x}\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} }−\frac{\mathrm{2}}{\mathrm{3}{x}^{\mathrm{3}} }+{o}\left(\frac{\mathrm{1}}{{x}^{\mathrm{4}} }\right)\right)\right] \\ $$$$=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)^{{x}} }×\left[{x}−{x}+\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}{x}}+\frac{\mathrm{2}}{\mathrm{3}{x}^{\mathrm{2}} }−{o}\left(\frac{\mathrm{1}}{{x}^{\mathrm{3}} }\right)\right] \\ $$$$=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)^{{x}} }×\left[\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}{x}}+\frac{\mathrm{2}}{\mathrm{3}{x}^{\mathrm{2}} }−{o}\left(\frac{\mathrm{1}}{{x}^{\mathrm{3}} }\right)\right] \\ $$$$=\frac{\mathrm{1}}{{e}} \\ $$
Commented by Adel last updated on 13/Jan/21

$$\mathrm{tanks} \\ $$
Commented by MJS_new last updated on 13/Jan/21

$$\mathrm{great}!\:\mathrm{I}\:\mathrm{came}\:\mathrm{to}\:\mathrm{the}\:\mathrm{2}^{\mathrm{nd}} \:\mathrm{line}\:\mathrm{but}\:\mathrm{then}\:\mathrm{had}\:\mathrm{no}\:\mathrm{idea}… \\ $$
Commented by Adel last updated on 16/Jan/21

$$ \\ $$
Commented by Adel last updated on 16/Jan/21

$$ \\ $$Which method did you use in the target section?
Commented by mr W last updated on 16/Jan/21

$${what}'{s}\:{that}\:{what}\:{you}\:{don}'{t}\:{understand}? \\ $$
Commented by Adel last updated on 16/Jan/21

$$\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{x}} \\ $$$$\mathrm{which}\:\mathrm{methode}\:\mathrm{uose}\:\mathrm{in}\:\mathrm{this}\:\mathrm{section}? \\ $$
Commented by mr W last updated on 16/Jan/21
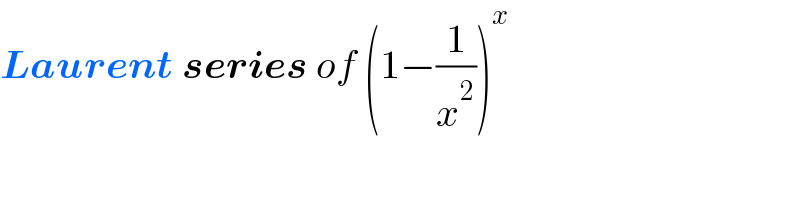
$$\boldsymbol{{Laurent}}\:\boldsymbol{{series}}\:{of}\:\left(\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)^{{x}} \\ $$
Commented by Adel last updated on 16/Jan/21

$$\mathrm{do}\:\mathrm{you}\:\mathrm{have}\:\mathrm{whatsapp}?\:\: \\ $$$$\mathrm{my}\:\mathrm{number}\:\mathrm{pleas}\:\mathrm{sms}\:\mathrm{me} \\ $$$$\mathrm{0093770176901} \\ $$
Commented by mr W last updated on 16/Jan/21

$${sorry},\:{if}\:{i}\:{can}\:{help}\:{you},\:{i}\:{can}\:{only} \\ $$$${help}\:{here}\:{in}\:{the}\:{forum},\:{nowhere} \\ $$$${else}.\:{besides},\:{i}\:{really}\:{don}'{t}\:{have}\: \\ $$$${whatsapp}. \\ $$
