Question Number 84130 by mahdi last updated on 09/Mar/20
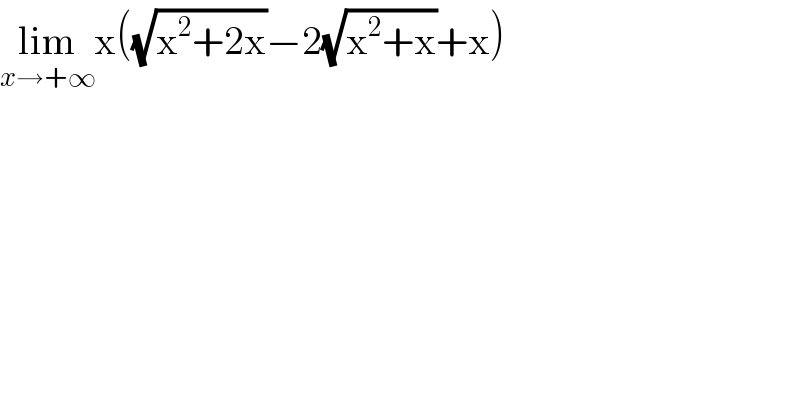
$$\underset{{x}\rightarrow+\infty} {\mathrm{lim}x}\left(\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{2x}}−\mathrm{2}\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}}+\mathrm{x}\right) \\ $$
Commented by MJS last updated on 10/Mar/20
![let x=(1/t) lim_(t→0^+ ) ((1/t)((√((1/t^2 )+(2/t)))−2(√((1/t^2 )+(1/t)))+(1/t))) = =lim_(t→0^+ ) ((1+(√(2t+1))−2(√(t+1)))/t^2 ) = =lim_(t→0^+ ) (((d^2 /dt^2 )[1+(√(2t+1))−2(√(t+1))])/((d^2 /dt^2 )[t^2 ])) = =lim_(t→0^+ ) (1/2)((1/(2(t+1)^(3/2) ))−(1/((2t+1)^(3/2) ))) = =(1/2)((1/2)−1)=−(1/4)](https://www.tinkutara.com/question/Q84168.png)
$$\mathrm{let}\:{x}=\frac{\mathrm{1}}{{t}} \\ $$$$\underset{{t}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\left(\frac{\mathrm{1}}{{t}}\left(\sqrt{\frac{\mathrm{1}}{{t}^{\mathrm{2}} }+\frac{\mathrm{2}}{{t}}}−\mathrm{2}\sqrt{\frac{\mathrm{1}}{{t}^{\mathrm{2}} }+\frac{\mathrm{1}}{{t}}}+\frac{\mathrm{1}}{{t}}\right)\right)\:= \\ $$$$=\underset{{t}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\frac{\mathrm{1}+\sqrt{\mathrm{2}{t}+\mathrm{1}}−\mathrm{2}\sqrt{{t}+\mathrm{1}}}{{t}^{\mathrm{2}} }\:= \\ $$$$=\underset{{t}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\frac{\frac{{d}^{\mathrm{2}} }{{dt}^{\mathrm{2}} }\left[\mathrm{1}+\sqrt{\mathrm{2}{t}+\mathrm{1}}−\mathrm{2}\sqrt{{t}+\mathrm{1}}\right]}{\frac{{d}^{\mathrm{2}} }{{dt}^{\mathrm{2}} }\left[{t}^{\mathrm{2}} \right]}\:= \\ $$$$=\underset{{t}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{2}\left({t}+\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }−\frac{\mathrm{1}}{\left(\mathrm{2}{t}+\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }\right)\:= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}\right)=−\frac{\mathrm{1}}{\mathrm{4}} \\ $$
Commented by mahdi last updated on 06/Apr/20

$$\mathrm{thank}\:\mathrm{you} \\ $$
