Question Number 162182 by bobhans last updated on 27/Dec/21
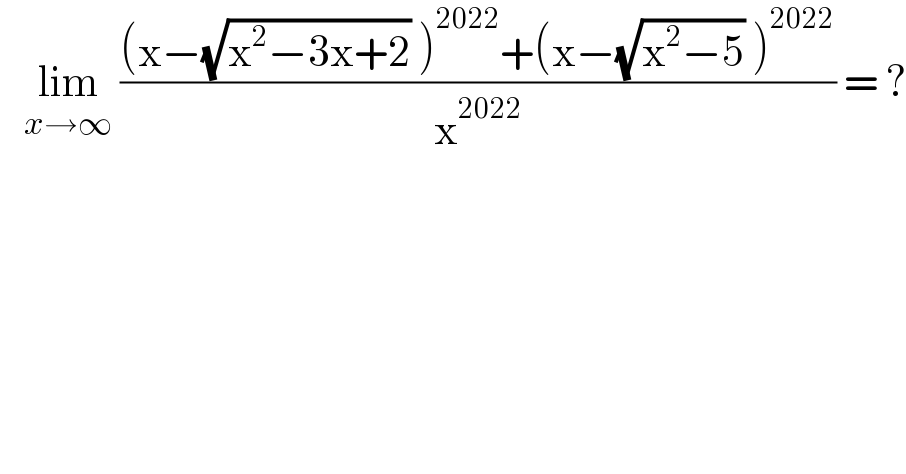
$$\:\:\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\left(\mathrm{x}−\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{3x}+\mathrm{2}}\:\right)^{\mathrm{2022}} +\left(\mathrm{x}−\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{5}}\:\right)^{\mathrm{2022}} }{\mathrm{x}^{\mathrm{2022}} }\:=\:? \\ $$
Answered by cortano last updated on 27/Dec/21
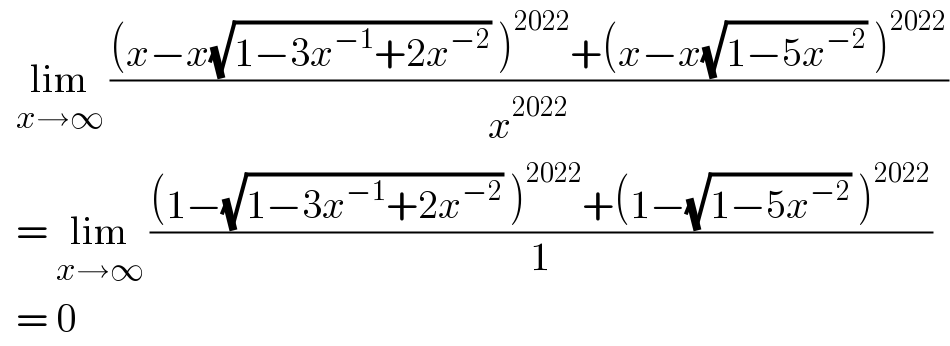
$$\:\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\left({x}−{x}\sqrt{\mathrm{1}−\mathrm{3}{x}^{−\mathrm{1}} +\mathrm{2}{x}^{−\mathrm{2}} }\:\right)^{\mathrm{2022}} +\left({x}−{x}\sqrt{\mathrm{1}−\mathrm{5}{x}^{−\mathrm{2}} }\:\right)^{\mathrm{2022}} }{{x}^{\mathrm{2022}} } \\ $$$$\:\:=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\left(\mathrm{1}−\sqrt{\mathrm{1}−\mathrm{3}{x}^{−\mathrm{1}} +\mathrm{2}{x}^{−\mathrm{2}} }\:\right)^{\mathrm{2022}} +\left(\mathrm{1}−\sqrt{\mathrm{1}−\mathrm{5}{x}^{−\mathrm{2}} }\:\right)^{\mathrm{2022}} }{\mathrm{1}} \\ $$$$\:\:=\:\mathrm{0}\: \\ $$
