Question Number 79565 by jagoll last updated on 26/Jan/20
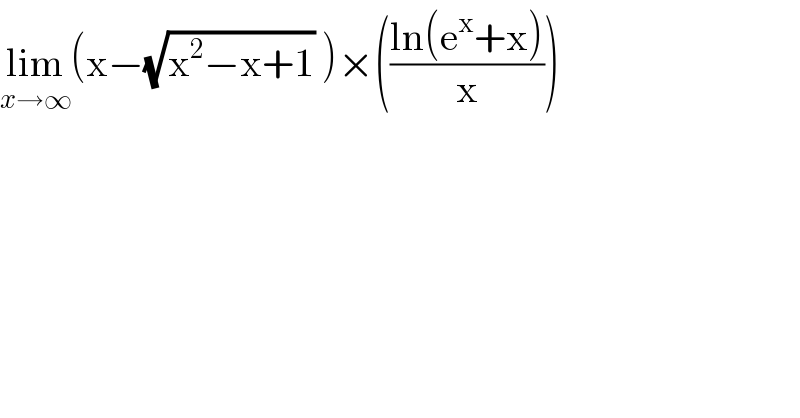
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{x}−\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}}\:\right)×\left(\frac{\mathrm{ln}\left(\mathrm{e}^{\mathrm{x}} +\mathrm{x}\right)}{\mathrm{x}}\right) \\ $$
Commented by john santu last updated on 26/Jan/20
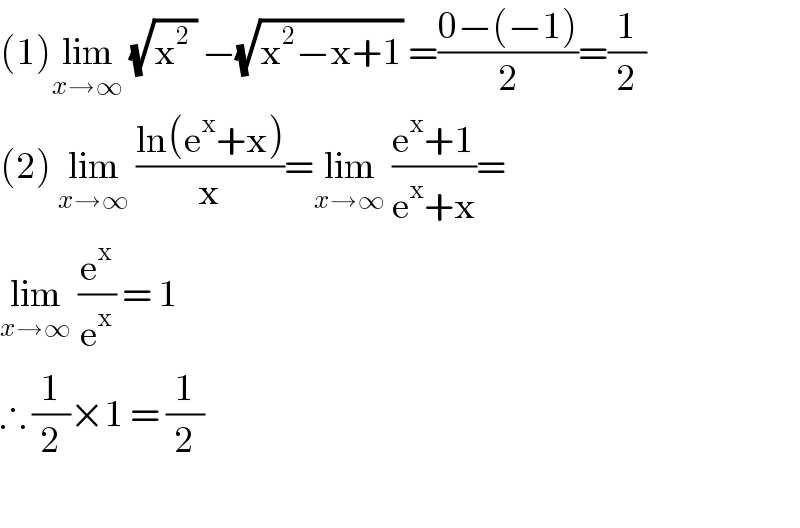
$$\left(\mathrm{1}\right)\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\sqrt{\mathrm{x}^{\mathrm{2}} \:}\:−\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}}\:=\frac{\mathrm{0}−\left(−\mathrm{1}\right)}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\left(\mathrm{2}\right)\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{ln}\left(\mathrm{e}^{\mathrm{x}} +\mathrm{x}\right)}{\mathrm{x}}=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{e}^{\mathrm{x}} +\mathrm{1}}{\mathrm{e}^{\mathrm{x}} +\mathrm{x}}= \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{e}^{\mathrm{x}} }{\mathrm{e}^{\mathrm{x}} }\:=\:\mathrm{1} \\ $$$$\therefore\:\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{1}\:=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 26/Jan/20
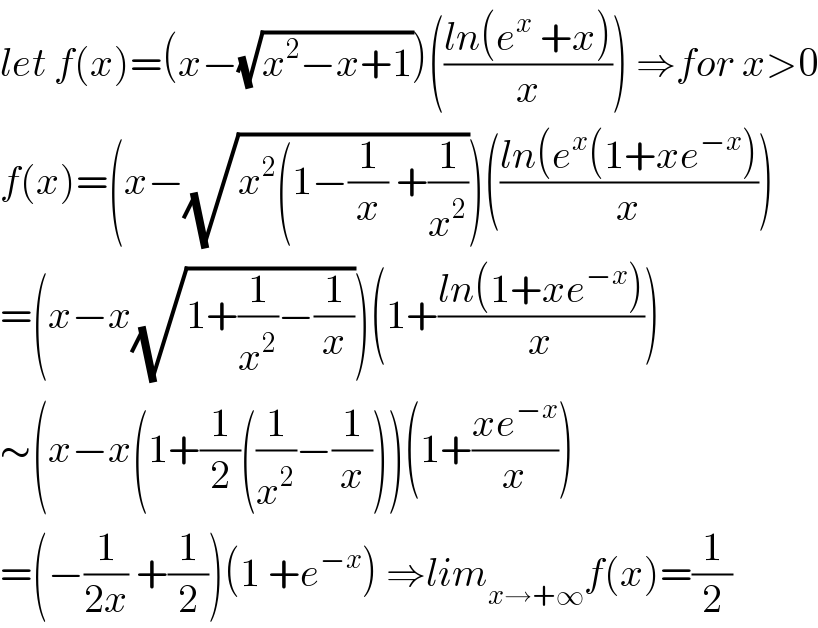
$${let}\:{f}\left({x}\right)=\left({x}−\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}\right)\left(\frac{{ln}\left({e}^{{x}} \:+{x}\right)}{{x}}\right)\:\Rightarrow{for}\:{x}>\mathrm{0} \\ $$$${f}\left({x}\right)=\left({x}−\sqrt{{x}^{\mathrm{2}} \left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\:+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right.}\right)\left(\frac{{ln}\left({e}^{{x}} \left(\mathrm{1}+{xe}^{−{x}} \right)\right.}{{x}}\right) \\ $$$$=\left({x}−{x}\sqrt{\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }−\frac{\mathrm{1}}{{x}}}\right)\left(\mathrm{1}+\frac{{ln}\left(\mathrm{1}+{xe}^{−{x}} \right)}{{x}}\right) \\ $$$$\sim\left({x}−{x}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} }−\frac{\mathrm{1}}{{x}}\right)\right)\left(\mathrm{1}+\frac{{xe}^{−{x}} }{{x}}\right)\right. \\ $$$$=\left(−\frac{\mathrm{1}}{\mathrm{2}{x}}\:+\frac{\mathrm{1}}{\mathrm{2}}\right)\left(\mathrm{1}\:+{e}^{−{x}} \right)\:\Rightarrow{lim}_{{x}\rightarrow+\infty} {f}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
