Question Number 126599 by liberty last updated on 22/Dec/20
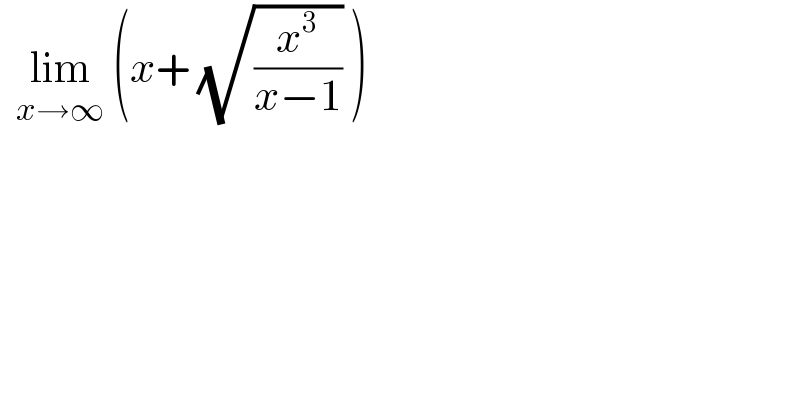
$$\:\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left({x}+\:\sqrt{\frac{{x}^{\mathrm{3}} }{{x}−\mathrm{1}}}\:\right) \\ $$
Answered by bramlexs22 last updated on 22/Dec/20
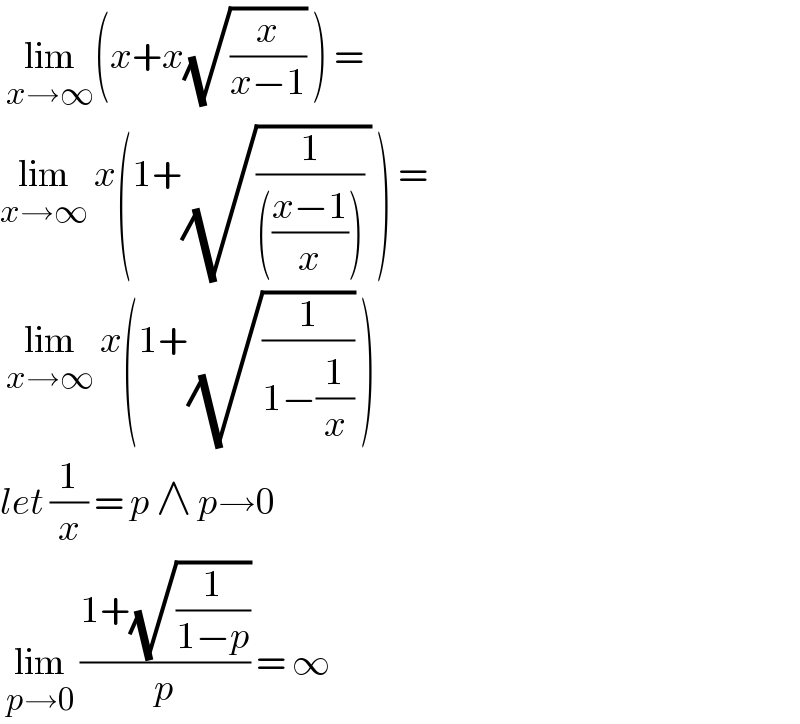
$$\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left({x}+{x}\sqrt{\frac{{x}}{{x}−\mathrm{1}}}\:\right)\:= \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:{x}\left(\mathrm{1}+\sqrt{\frac{\mathrm{1}}{\left(\frac{{x}−\mathrm{1}}{{x}}\right)}\:}\:\right)\:= \\ $$$$\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:{x}\left(\mathrm{1}+\sqrt{\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}}{{x}}}}\:\right)\: \\ $$$${let}\:\frac{\mathrm{1}}{{x}}\:=\:{p}\:\wedge\:{p}\rightarrow\mathrm{0} \\ $$$$\:\underset{{p}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}+\sqrt{\frac{\mathrm{1}}{\mathrm{1}−{p}}}}{{p}}\:=\:\infty\: \\ $$
