Question Number 128992 by liberty last updated on 12/Jan/21
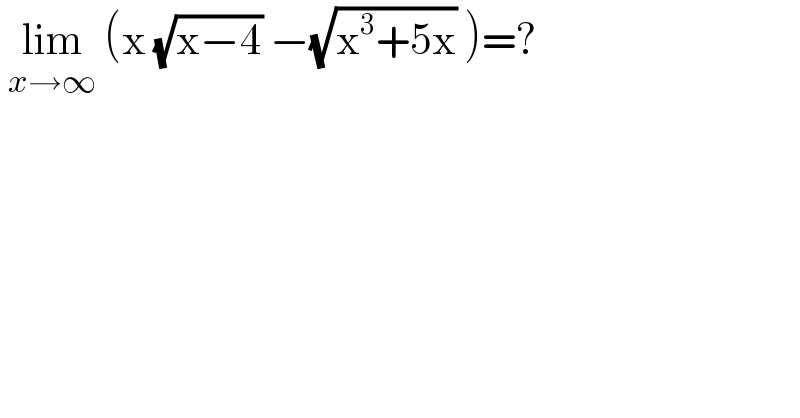
$$\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left(\mathrm{x}\:\sqrt{\mathrm{x}−\mathrm{4}}\:−\sqrt{\mathrm{x}^{\mathrm{3}} +\mathrm{5x}}\:\right)=? \\ $$
Answered by bramlexs22 last updated on 12/Jan/21
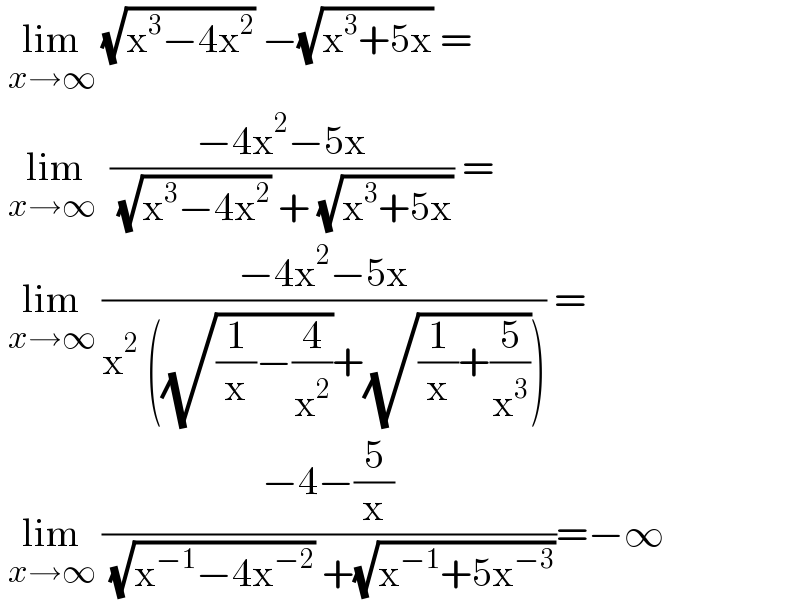
$$\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\sqrt{\mathrm{x}^{\mathrm{3}} −\mathrm{4x}^{\mathrm{2}} }\:−\sqrt{\mathrm{x}^{\mathrm{3}} +\mathrm{5x}}\:= \\ $$$$\:\underset{{x}\rightarrow\infty\:} {\mathrm{lim}}\:\frac{−\mathrm{4x}^{\mathrm{2}} −\mathrm{5x}}{\:\sqrt{\mathrm{x}^{\mathrm{3}} −\mathrm{4x}^{\mathrm{2}} }\:+\:\sqrt{\mathrm{x}^{\mathrm{3}} +\mathrm{5x}}}\:= \\ $$$$\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{−\mathrm{4x}^{\mathrm{2}} −\mathrm{5x}}{\mathrm{x}^{\mathrm{2}} \:\left(\sqrt{\frac{\mathrm{1}}{\mathrm{x}}−\frac{\mathrm{4}}{\mathrm{x}^{\mathrm{2}} }}+\sqrt{\frac{\mathrm{1}}{\mathrm{x}}+\frac{\mathrm{5}}{\mathrm{x}^{\mathrm{3}} }}\right)}\:= \\ $$$$\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{−\mathrm{4}−\frac{\mathrm{5}}{\mathrm{x}}}{\:\sqrt{\mathrm{x}^{−\mathrm{1}} −\mathrm{4x}^{−\mathrm{2}} }\:+\sqrt{\mathrm{x}^{−\mathrm{1}} +\mathrm{5x}^{−\mathrm{3}} }}=−\infty \\ $$
