Question Number 34921 by rahul 19 last updated on 13/May/18
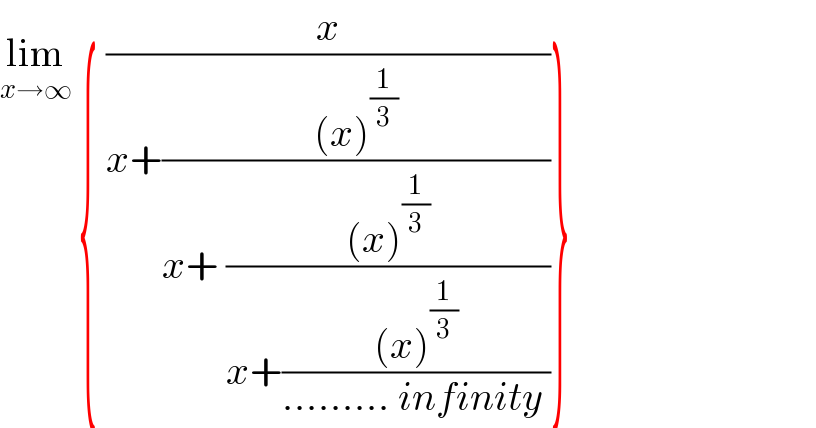
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left\{\:\frac{{x}}{{x}+\frac{\left({x}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} }{{x}+\:\frac{\left({x}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} }{{x}+\frac{\left({x}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} }{………\:{infinity}\:}}}}\right\} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 13/May/18
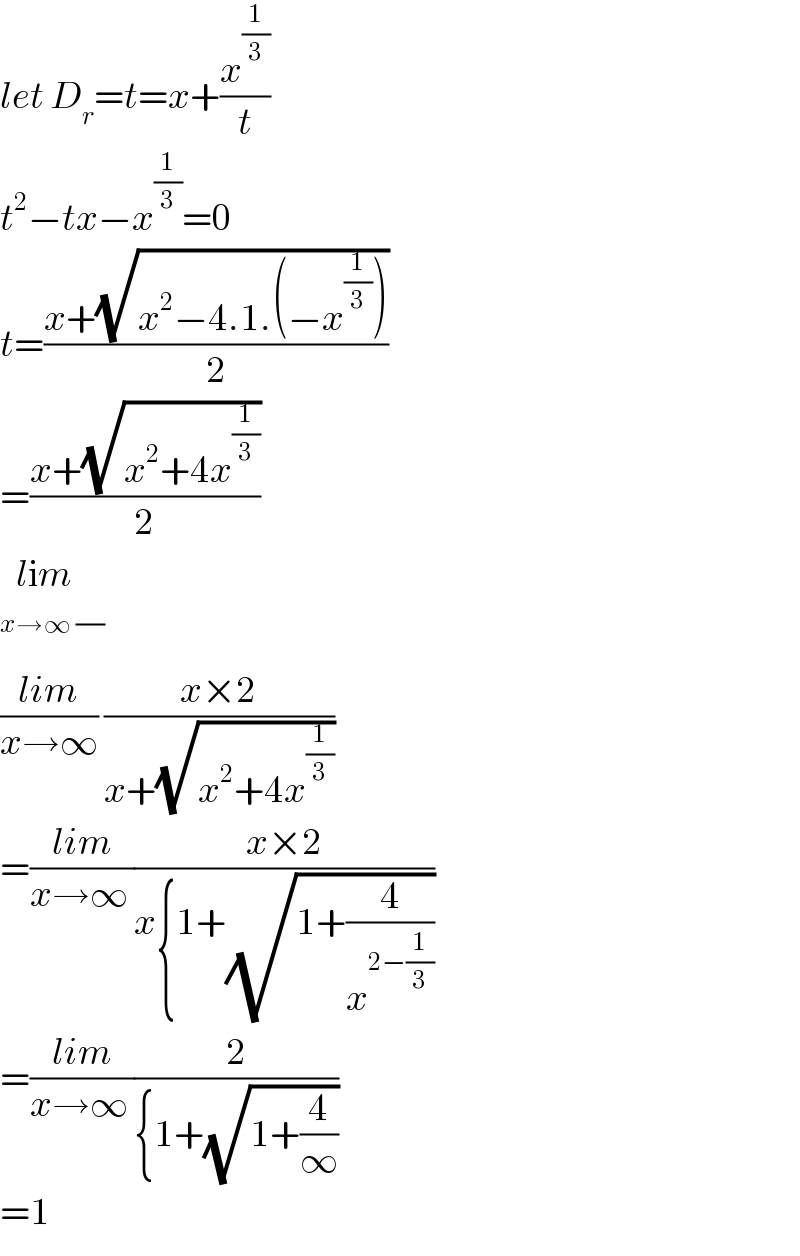
$${let}\:{D}_{{r}} ={t}={x}+\frac{{x}^{\frac{\mathrm{1}}{\mathrm{3}}} }{{t}} \\ $$$${t}^{\mathrm{2}} −{tx}−{x}^{\frac{\mathrm{1}}{\mathrm{3}}} =\mathrm{0} \\ $$$${t}=\frac{{x}+\sqrt{{x}^{\mathrm{2}} −\mathrm{4}.\mathrm{1}.\left(−{x}^{\frac{\mathrm{1}}{\mathrm{3}}} \right)}}{\mathrm{2}} \\ $$$$=\frac{{x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{4}{x}^{\frac{\mathrm{1}}{\mathrm{3}}} }}{\mathrm{2}} \\ $$$$\underset{{x}\rightarrow\infty\:\frac{}{}} {{l}\mathrm{i}{m}} \\ $$$$\frac{{lim}}{{x}\rightarrow\infty}\:\frac{{x}×\mathrm{2}}{{x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{4}{x}^{\frac{\mathrm{1}}{\mathrm{3}}} }} \\ $$$$=\frac{{lim}}{{x}\rightarrow\infty\:}\frac{{x}×\mathrm{2}}{{x}\left\{\mathrm{1}+\sqrt{\mathrm{1}+\frac{\mathrm{4}}{{x}^{\mathrm{2}−\frac{\mathrm{1}}{\mathrm{3}}} }}\right.} \\ $$$$=\frac{{lim}}{{x}\rightarrow\infty\:}\frac{\mathrm{2}}{\left\{\mathrm{1}+\sqrt{\mathrm{1}+\frac{\mathrm{4}}{\infty}}\right.} \\ $$$$=\mathrm{1} \\ $$
Commented by rahul 19 last updated on 13/May/18

$${Thank}\:{you}\:{sir}. \\ $$
Commented by NECx last updated on 15/May/18

$${wow} \\ $$
