lim-x-x-x-x-1-x-

Question Number 80748 by jagoll last updated on 06/Feb/20

\lim_{x \to \infty} {(\frac{x!}{x^{x}})}^{\frac{1}{x}} = ?

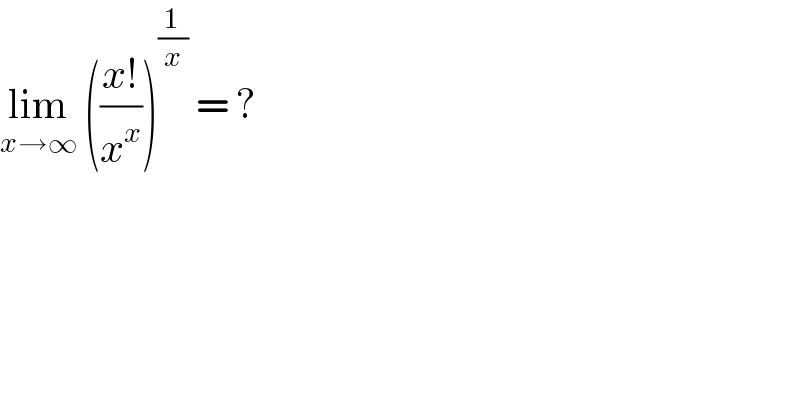
Commented by john santu last updated on 06/Feb/20

l e t y = \lim_{x \to \infty} {(\frac{x!}{x^{x}})}^{\frac{1}{x}}

l n (y) = \lim_{x \to \infty} l n {(\frac{x!}{x^{x}})}^{\frac{1}{x}}

l n (y) = \lim_{x \to \infty} l n {(\frac{x!}{x^{x}})}^{\frac{1}{x}}

l n (y) = \lim_{x \to \infty} \frac{1}{x} l n (\frac{x!}{x^{x}})

= \lim_{x \to \infty} \frac{1}{x} (l n (\frac{1}{x}) + l n (\frac{2}{x}) + \dots + l n (\frac{x - 1}{x}) + l n (\frac{x}{x}))

= \int_{0}^{1} l n (x) d x = - 1

l n (y) = - 1 \Rightarrow ∴ y = e^{- 1}

\lim_{x \to \infty} {(\frac{x!}{x^{x}})}^{\frac{1}{x}} = \frac{1}{e}

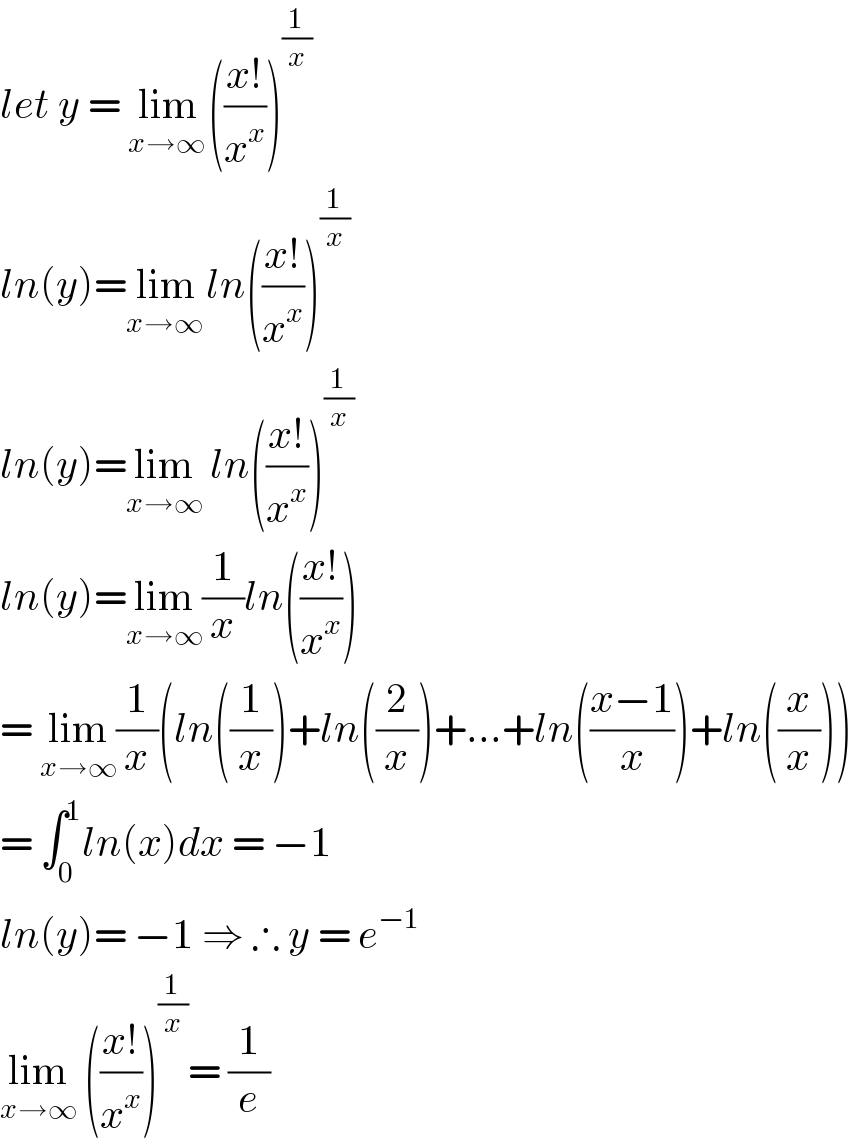
Commented by jagoll last updated on 06/Feb/20

t h a n k s

Commented by mathmax by abdo last updated on 06/Feb/20

l e t f (x) = {(\frac{x!}{x^{x}})}^{\frac{1}{x}} w e h a v e x! \sim x^{x} e^{- x} \sqrt{2 π x} (x \to + \infty) \Rightarrow

f (x) \sim {(e^{- x} \sqrt{2 π x})}^{\frac{1}{x}} = e^{\frac{1}{x} l n (e^{- x} \sqrt{2 π x})} = e^{- 1 + \frac{1}{2 x} l n (2 π x)} \Rightarrow e^{- 1} = \frac{1}{e} (x \to + \infty)

\Rightarrow {l i m}_{x \to + \infty} f (x) = \frac{1}{e}

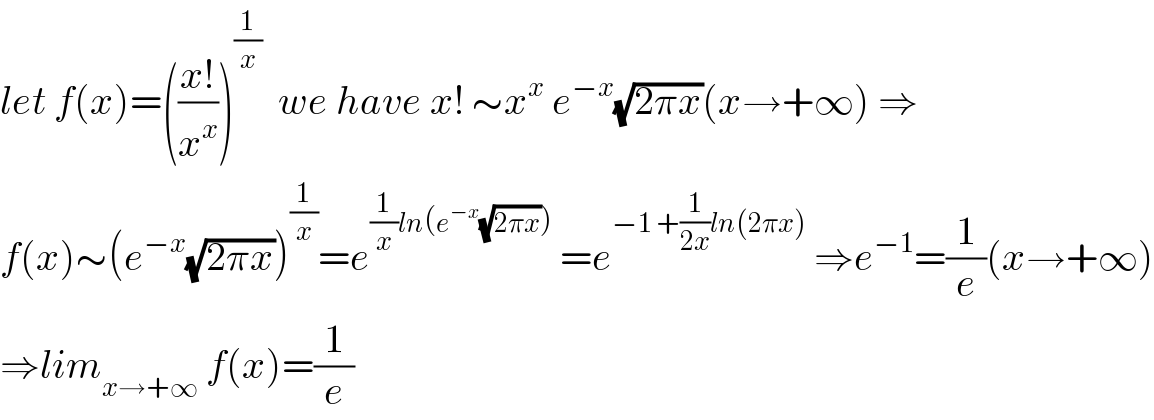
Answered by MJS last updated on 06/Feb/20

\lim_{x \to \infty} {(\frac{x!}{x^{x}})}^{\frac{1}{x}} =

[x! \approx \frac{x^{x}}{e^{x}} \sqrt{2 π x} {Sterling}^{'} s approximation]

= \frac{1}{e} \lim_{x \to \infty} {(2 π x)}^{\frac{1}{2 x}} = \frac{1}{e}

[\lim_{x \to \infty} C_{1}^{\frac{1}{x}} = 1 \forall C_{1} > 0]

[\lim_{x \to \infty} x^{\frac{1}{C_{2} x}} = \lim_{x \to \infty} e^{\frac{\ln x}{C_{2} x}} = 10^{0} = 1 \forall C_{2} \neq 0]

Commented by jagoll last updated on 06/Feb/20

m i s t e r t h e a n s w e r \frac{1}{e} m i s t e r

w h a t w r o n g ?

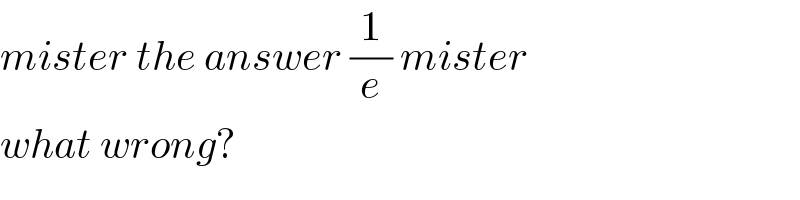
Commented by MJS last updated on 06/Feb/20

the answer is there in line 3

Commented by jagoll last updated on 06/Feb/20

o o t h a n k y o u m i s t e r . i s e e t h e

l a s t l i n e

Facebook Tweet Pin