Question Number 117037 by bemath last updated on 09/Oct/20
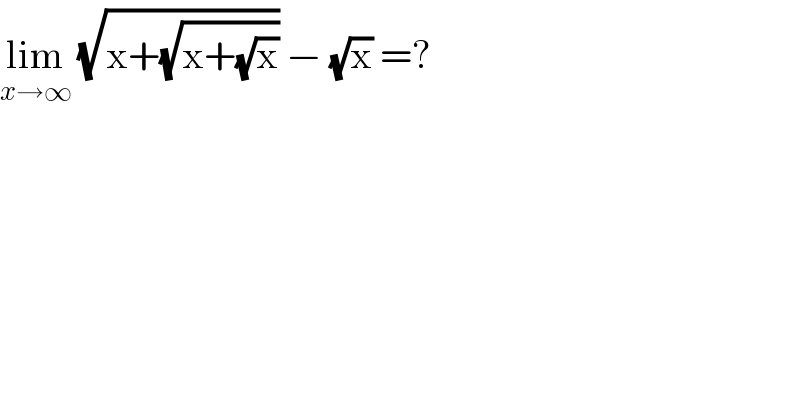
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\sqrt{\mathrm{x}+\sqrt{\mathrm{x}+\sqrt{\mathrm{x}}}}\:−\:\sqrt{\mathrm{x}}\:=?\: \\ $$
Answered by Lordose last updated on 09/Oct/20

$$\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Answered by bobhans last updated on 09/Oct/20
![lim_(x→∞) (√(x+(√(x+(√x))))) − (√x) = lim_(x→∞) (√(x(1+((√(x+(√x)))/x)))) − (√x) = lim_(x→∞) (√x) [(√(1+(√((1/x)+(√(1/x^3 )))))) − 1 ]= let (√x) = (1/t) or x = (1/t^2 ) where t→0 lim_(t→0) (((√(1+(√(t^2 +(√t^6 ))) )) −1)/t) = lim_(t→0) (1/( (√(1+(√(t^2 +(√t^6 ))))) + 1)) × lim_(t→0) ((√(t^2 +(√t^6 )))/t) = (1/2) × lim_(t→0) ((t(√(1+(√t^2 ))))/t) = (1/2)×1=(1/2)](https://www.tinkutara.com/question/Q117044.png)
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\sqrt{\mathrm{x}+\sqrt{\mathrm{x}+\sqrt{\mathrm{x}}}}\:−\:\sqrt{\mathrm{x}}\:= \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\sqrt{\mathrm{x}\left(\mathrm{1}+\frac{\sqrt{\mathrm{x}+\sqrt{\mathrm{x}}}}{\mathrm{x}}\right)}\:−\:\sqrt{\mathrm{x}}\:= \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\sqrt{\mathrm{x}}\:\left[\sqrt{\mathrm{1}+\sqrt{\frac{\mathrm{1}}{\mathrm{x}}+\sqrt{\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{3}} }}}}\:−\:\mathrm{1}\:\right]= \\ $$$$\mathrm{let}\:\sqrt{\mathrm{x}}\:=\:\frac{\mathrm{1}}{\mathrm{t}}\:\mathrm{or}\:\mathrm{x}\:=\:\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }\:\mathrm{where}\:\mathrm{t}\rightarrow\mathrm{0} \\ $$$$\underset{\mathrm{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{1}+\sqrt{\mathrm{t}^{\mathrm{2}} +\sqrt{\mathrm{t}^{\mathrm{6}} }}\:}\:−\mathrm{1}}{\mathrm{t}}\:=\: \\ $$$$\underset{\mathrm{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\sqrt{\mathrm{t}^{\mathrm{2}} +\sqrt{\mathrm{t}^{\mathrm{6}} }}}\:+\:\mathrm{1}}\:×\:\underset{\mathrm{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\sqrt{\mathrm{t}^{\mathrm{2}} +\sqrt{\mathrm{t}^{\mathrm{6}} }}}{\mathrm{t}}\:= \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\:×\:\underset{\mathrm{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{t}\sqrt{\mathrm{1}+\sqrt{\mathrm{t}^{\mathrm{2}} }}}{\mathrm{t}}\:=\:\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{1}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Answered by Dwaipayan Shikari last updated on 09/Oct/20
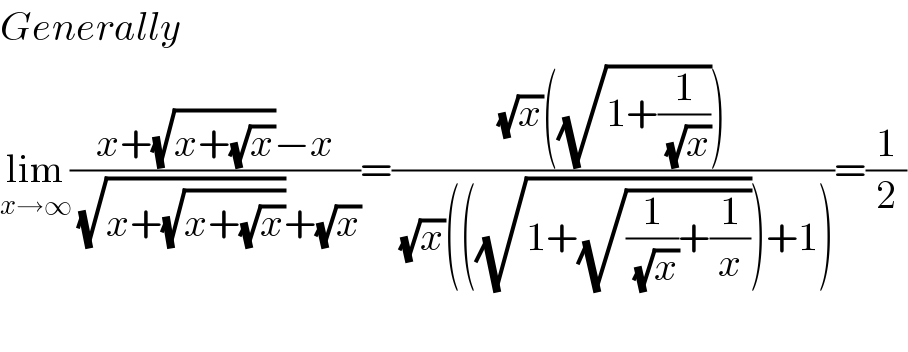
$${Generally} \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{{x}+\sqrt{{x}+\sqrt{{x}}}−{x}}{\:\sqrt{{x}+\sqrt{{x}+\sqrt{{x}}}}+\sqrt{{x}}}=\frac{\sqrt{{x}}\left(\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\:\sqrt{{x}}}}\right)}{\:\sqrt{{x}}\left(\left(\sqrt{\mathrm{1}+\sqrt{\frac{\mathrm{1}}{\:\sqrt{{x}}}+\frac{\mathrm{1}}{{x}}}}\right)+\mathrm{1}\right)}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$ \\ $$
