lim-x-x-x-x-zaynal-

Question Number 163666 by Zaynal last updated on 09/Jan/22

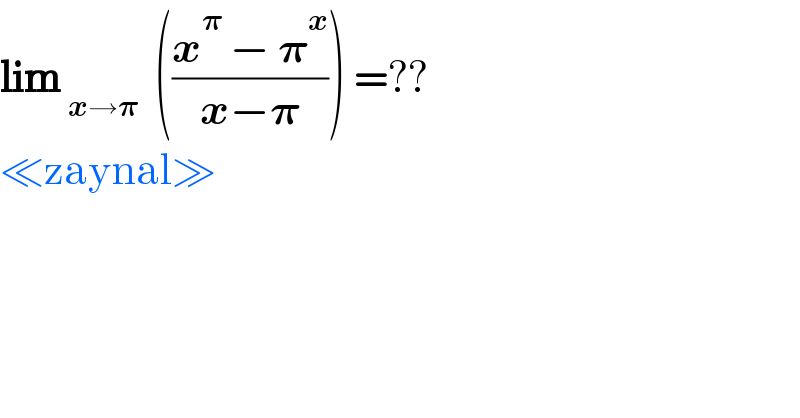
lim _(x→𝛑) (((x^𝛑 − 𝛑^x )/(x−𝛑))) =?? ≪zaynal≫

$$\boldsymbol{\mathrm{lim}}\:_{\boldsymbol{{x}}\rightarrow\boldsymbol{\pi}} \:\:\left(\frac{\boldsymbol{{x}}^{\boldsymbol{\pi}} \:−\:\boldsymbol{\pi}^{\boldsymbol{{x}}} }{\boldsymbol{{x}}−\boldsymbol{\pi}}\right)\:=?? \\ $$$$\ll\mathrm{zaynal}\gg \\ $$

Answered by mahdipoor last updated on 09/Jan/22

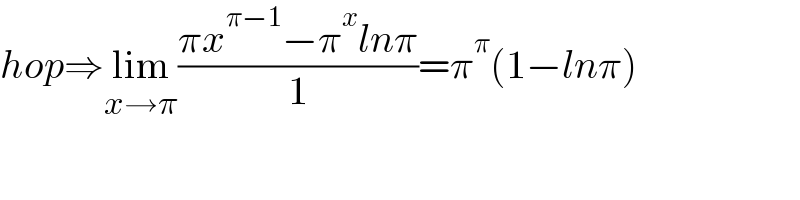
hop⇒lim_(x→π) ((πx^(π−1) −π^x lnπ)/1)=π^π (1−lnπ)

$${hop}\Rightarrow\underset{{x}\rightarrow\pi} {\mathrm{lim}}\frac{\pi{x}^{\pi−\mathrm{1}} −\pi^{{x}} {ln}\pi}{\mathrm{1}}=\pi^{\pi} \left(\mathrm{1}−{ln}\pi\right) \\ $$

Answered by Ar Brandon last updated on 09/Jan/22

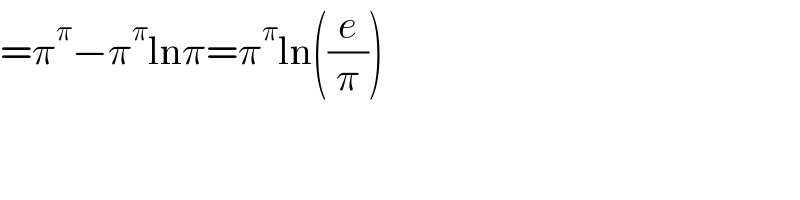
$$=\pi^{\pi} −\pi^{\pi} \mathrm{ln}\pi=\pi^{\pi} \mathrm{ln}\left(\frac{{e}}{\pi}\right) \\ $$

Commented by Zaynal last updated on 09/Jan/22

$$\mathrm{ok}\: \\ $$

Answered by alephzero last updated on 09/Jan/22

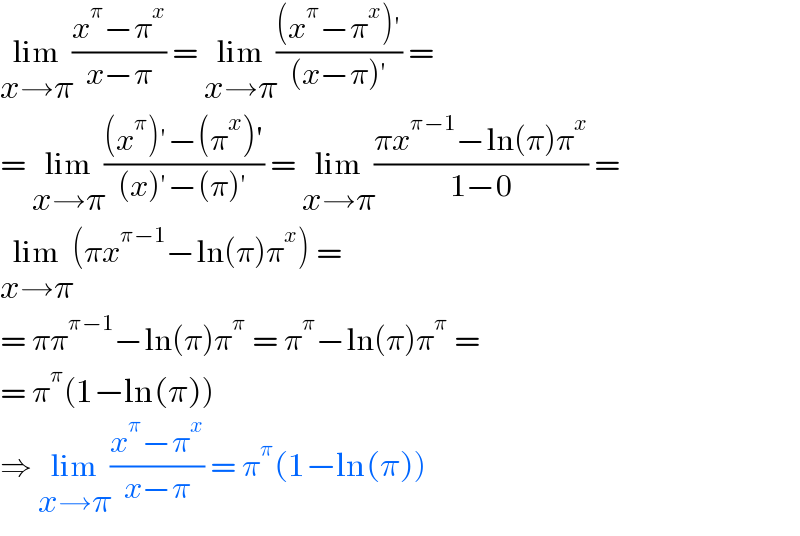
lim_(x→π) ((x^π −π^x )/(x−π)) = lim_(x→π) (((x^π −π^x )′)/((x−π)′)) = = lim_(x→π) (((x^π )′−(π^x )′)/((x)′−(π)′)) = lim_(x→π) ((πx^(π−1) −ln(π)π^x )/(1−0)) = lim_(x→π) (πx^(π−1) −ln(π)π^x ) = = ππ^(π−1) −ln(π)π^π = π^π −ln(π)π^π = = π^π (1−ln(π)) ⇒ lim_(x→π) ((x^π −π^x )/(x−π)) = π^π (1−ln(π))

$$\underset{{x}\rightarrow\pi} {\mathrm{lim}}\frac{{x}^{\pi} −\pi^{{x}} }{{x}−\pi}\:=\:\underset{{x}\rightarrow\pi} {\mathrm{lim}}\frac{\left({x}^{\pi} −\pi^{{x}} \right)'}{\left({x}−\pi\right)'}\:= \\ $$$$=\:\underset{{x}\rightarrow\pi} {\mathrm{lim}}\frac{\left({x}^{\pi} \right)'−\left(\pi^{{x}} \right)'}{\left({x}\right)'−\left(\pi\right)'}\:=\:\underset{{x}\rightarrow\pi} {\mathrm{lim}}\frac{\pi{x}^{\pi−\mathrm{1}} −\mathrm{ln}\left(\pi\right)\pi^{{x}} }{\mathrm{1}−\mathrm{0}}\:= \\ $$$$\underset{{x}\rightarrow\pi} {\mathrm{lim}}\left(\pi{x}^{\pi−\mathrm{1}} −\mathrm{ln}\left(\pi\right)\pi^{{x}} \right)\:= \\ $$$$=\:\pi\pi^{\pi−\mathrm{1}} −\mathrm{ln}\left(\pi\right)\pi^{\pi} \:=\:\pi^{\pi} −\mathrm{ln}\left(\pi\right)\pi^{\pi} \:= \\ $$$$=\:\pi^{\pi} \left(\mathrm{1}−\mathrm{ln}\left(\pi\right)\right) \\ $$$$\Rightarrow\:\underset{{x}\rightarrow\pi} {\mathrm{lim}}\frac{{x}^{\pi} −\pi^{{x}} }{{x}−\pi}\:=\:\pi^{\pi} \left(\mathrm{1}−\mathrm{ln}\left(\pi\right)\right) \\ $$

Answered by manxsolar last updated on 16/Jan/22

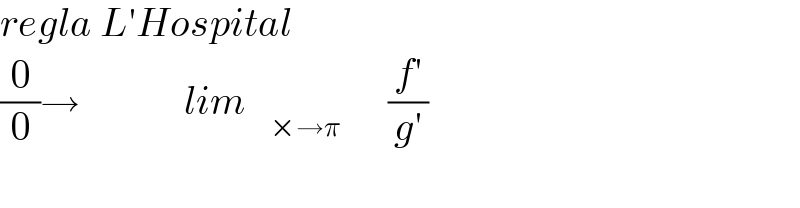
regla L′Hospital (0/0)→ lim _(×→π) ((f′)/(g′))

$${regla}\:{L}'{Hospital} \\ $$$$\frac{\mathrm{0}}{\mathrm{0}}\rightarrow\:\:\:\:\:\:\:\:\:\:\:\:\:{lim}\:\:\:_{×\rightarrow\pi} \:\:\:\:\:\:\frac{{f}'}{{g}'} \\ $$$$ \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply