Question Number 114790 by manuel2456 last updated on 21/Sep/20
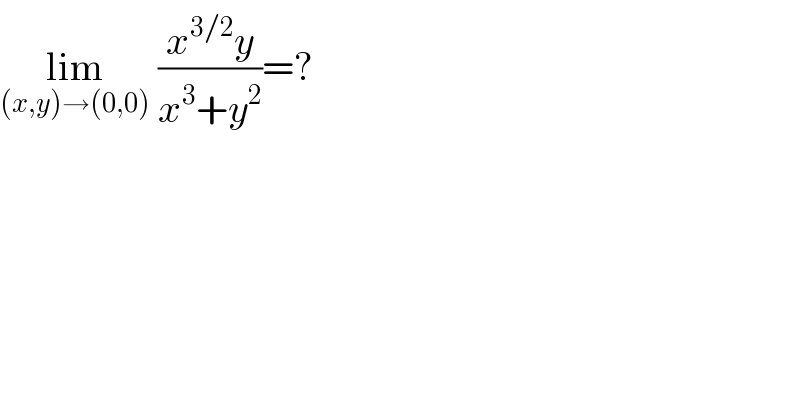
$$\underset{\left({x},{y}\right)\rightarrow\left(\mathrm{0},\mathrm{0}\right)} {\mathrm{lim}}\:\frac{{x}^{\mathrm{3}/\mathrm{2}} {y}}{{x}^{\mathrm{3}} +{y}^{\mathrm{2}} }=? \\ $$
Answered by Olaf last updated on 26/Sep/20
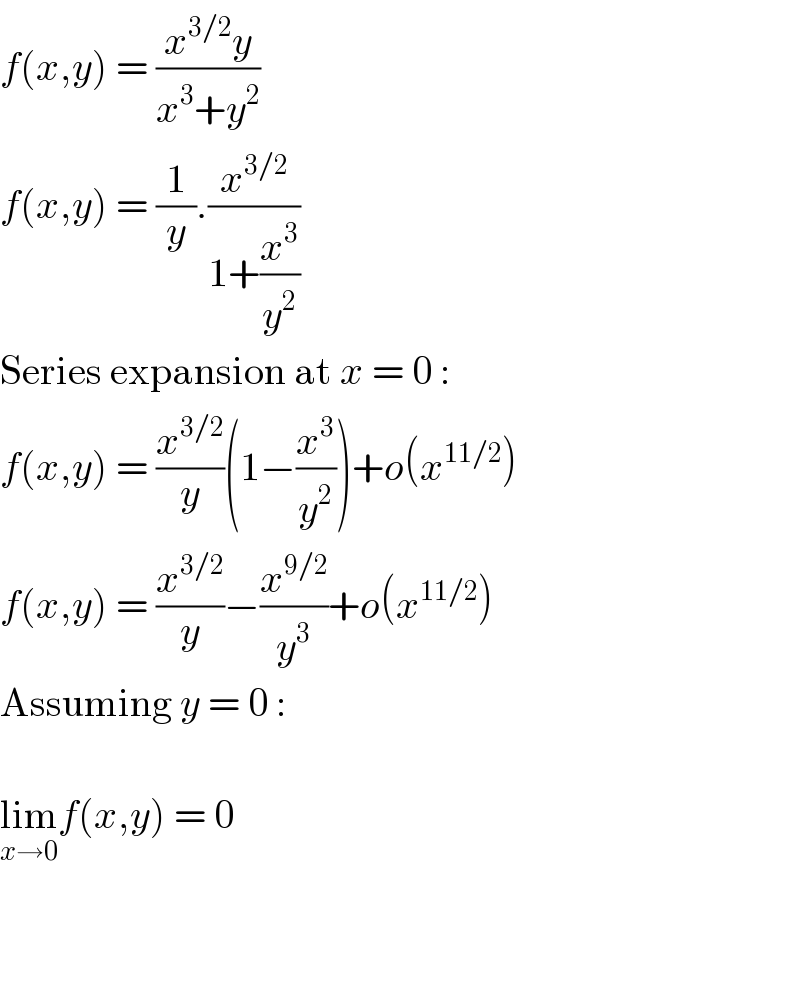
$${f}\left({x},{y}\right)\:=\:\frac{{x}^{\mathrm{3}/\mathrm{2}} {y}}{{x}^{\mathrm{3}} +{y}^{\mathrm{2}} } \\ $$$${f}\left({x},{y}\right)\:=\:\frac{\mathrm{1}}{{y}}.\frac{{x}^{\mathrm{3}/\mathrm{2}} }{\mathrm{1}+\frac{{x}^{\mathrm{3}} }{{y}^{\mathrm{2}} }} \\ $$$$\mathrm{Series}\:\mathrm{expansion}\:\mathrm{at}\:{x}\:=\:\mathrm{0}\:: \\ $$$${f}\left({x},{y}\right)\:=\:\frac{{x}^{\mathrm{3}/\mathrm{2}} }{{y}}\left(\mathrm{1}−\frac{{x}^{\mathrm{3}} }{{y}^{\mathrm{2}} }\right)+{o}\left({x}^{\mathrm{11}/\mathrm{2}} \right) \\ $$$${f}\left({x},{y}\right)\:=\:\frac{{x}^{\mathrm{3}/\mathrm{2}} }{{y}}−\frac{{x}^{\mathrm{9}/\mathrm{2}} }{{y}^{\mathrm{3}} }+{o}\left({x}^{\mathrm{11}/\mathrm{2}} \right) \\ $$$$\mathrm{Assuming}\:{y}\:=\:\mathrm{0}\:: \\ $$$$ \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}{f}\left({x},{y}\right)\:=\:\mathrm{0} \\ $$$$ \\ $$$$ \\ $$
