lim-x-y-pi-2-arctan-x-2-y-2-1-ln-x-2-y-2-

Question Number 129120 by liberty last updated on 13/Jan/21

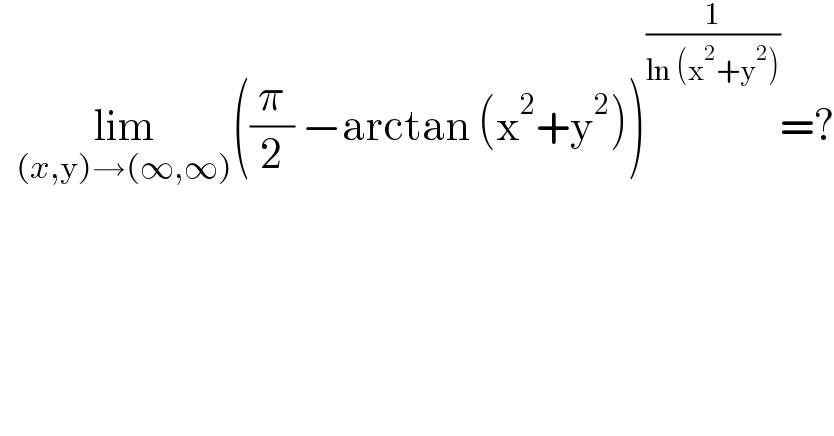
lim_((x,y)→(∞,∞)) ((π/2) −arctan (x^2 +y^2 ))^(1/(ln (x^2 +y^2 ))) =?

$$\:\:\underset{\left({x},\mathrm{y}\right)\rightarrow\left(\infty,\infty\right)} {\mathrm{lim}}\left(\frac{\pi}{\mathrm{2}}\:−\mathrm{arctan}\:\left(\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \right)\right)^{\frac{\mathrm{1}}{\mathrm{ln}\:\left(\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \right)}} =? \\ $$

Answered by benjo_mathlover last updated on 13/Jan/21

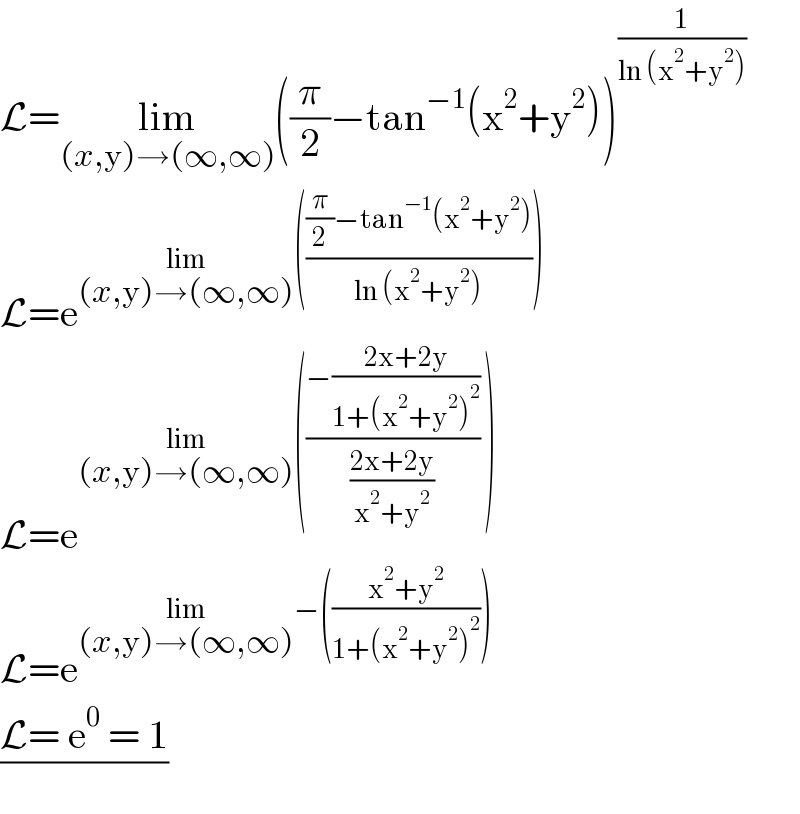
L=lim_((x,y)→(∞,∞)) ((π/2)−tan^(−1) (x^2 +y^2 ))^(1/(ln (x^2 +y^2 ))) L=e^(lim_((x,y)→(∞,∞)) ((((π/2)−tan^(−1) (x^2 +y^2 ))/(ln (x^2 +y^2 ))))) L=e^(lim_((x,y)→(∞,∞)) (((−((2x+2y)/(1+(x^2 +y^2 )^2 )))/((2x+2y)/(x^2 +y^2 ))) )) L=e^(lim_((x,y)→(∞,∞)) −(((x^2 +y^2 )/(1+(x^2 +y^2 )^2 )))) ((L= e^0 = 1)/)

$$\mathcal{L}=\underset{\left({x},\mathrm{y}\right)\rightarrow\left(\infty,\infty\right)} {\mathrm{lim}}\left(\frac{\pi}{\mathrm{2}}−\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \right)\right)^{\frac{\mathrm{1}}{\mathrm{ln}\:\left(\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \right)}} \\ $$$$\mathcal{L}=\mathrm{e}^{\underset{\left({x},\mathrm{y}\right)\rightarrow\left(\infty,\infty\right)} {\mathrm{lim}}\left(\frac{\frac{\pi}{\mathrm{2}}−\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \right)}{\mathrm{ln}\:\left(\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \right)}\right)} \\ $$$$\mathcal{L}=\mathrm{e}^{\underset{\left({x},\mathrm{y}\right)\rightarrow\left(\infty,\infty\right)} {\mathrm{lim}}\left(\frac{−\frac{\mathrm{2x}+\mathrm{2y}}{\mathrm{1}+\left(\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \right)^{\mathrm{2}} }}{\frac{\mathrm{2x}+\mathrm{2y}}{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} }}\:\right)} \\ $$$$\mathcal{L}=\mathrm{e}^{\underset{\left({x},\mathrm{y}\right)\rightarrow\left(\infty,\infty\right)} {\mathrm{lim}}−\left(\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} }{\mathrm{1}+\left(\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \right)^{\mathrm{2}} }\right)} \\ $$$$\frac{\mathcal{L}=\:\mathrm{e}^{\mathrm{0}} \:=\:\mathrm{1}}{} \\ $$

Answered by mathmax by abdo last updated on 14/Jan/21

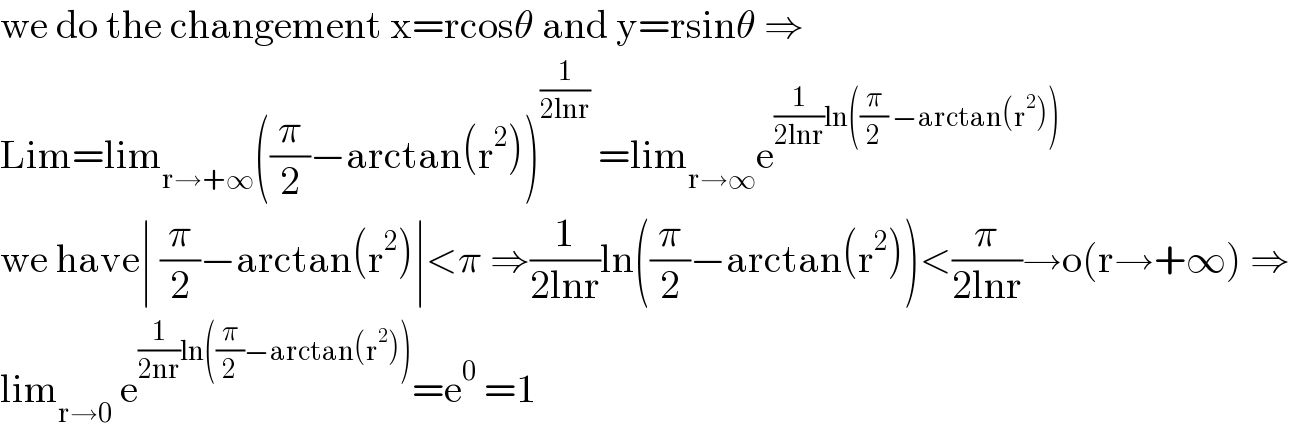
we do the changement x=rcosθ and y=rsinθ ⇒ Lim=lim_(r→+∞) ((π/2)−arctan(r^2 ))^(1/(2lnr)) =lim_(r→∞) e^((1/(2lnr))ln((π/2) −arctan(r^2 ))) we have∣ (π/2)−arctan(r^2 )∣<π ⇒(1/(2lnr))ln((π/2)−arctan(r^2 ))<(π/(2lnr))→o(r→+∞) ⇒ lim_(r→0) e^((1/(2nr))ln((π/2)−arctan(r^2 ))) =e^0 =1

$$\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\mathrm{x}=\mathrm{rcos}\theta\:\mathrm{and}\:\mathrm{y}=\mathrm{rsin}\theta\:\Rightarrow \\ $$$$\mathrm{Lim}=\mathrm{lim}_{\mathrm{r}\rightarrow+\infty} \left(\frac{\pi}{\mathrm{2}}−\mathrm{arctan}\left(\mathrm{r}^{\mathrm{2}} \right)\right)^{\frac{\mathrm{1}}{\mathrm{2lnr}}} \:=\mathrm{lim}_{\mathrm{r}\rightarrow\infty} \mathrm{e}^{\frac{\mathrm{1}}{\mathrm{2lnr}}\mathrm{ln}\left(\frac{\pi}{\mathrm{2}}\:−\mathrm{arctan}\left(\mathrm{r}^{\mathrm{2}} \right)\right)} \\ $$$$\mathrm{we}\:\mathrm{have}\mid\:\frac{\pi}{\mathrm{2}}−\mathrm{arctan}\left(\mathrm{r}^{\mathrm{2}} \right)\mid<\pi\:\Rightarrow\frac{\mathrm{1}}{\mathrm{2lnr}}\mathrm{ln}\left(\frac{\pi}{\mathrm{2}}−\mathrm{arctan}\left(\mathrm{r}^{\mathrm{2}} \right)\right)<\frac{\pi}{\mathrm{2lnr}}\rightarrow\mathrm{o}\left(\mathrm{r}\rightarrow+\infty\right)\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{r}\rightarrow\mathrm{0}} \:\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{2nr}}\mathrm{ln}\left(\frac{\pi}{\mathrm{2}}−\mathrm{arctan}\left(\mathrm{r}^{\mathrm{2}} \right)\right)} =\mathrm{e}^{\mathrm{0}} \:=\mathrm{1} \\ $$

Commented by mathmax by abdo last updated on 14/Jan/21

$$\mathrm{0}<\theta<\frac{\pi}{\mathrm{2}} \\ $$

Facebook Tweet Pin

lim-x-y-pi-2-arctan-x-2-y-2-1-ln-x-2-y-2-

Leave a Reply Cancel reply