lim-z-0-z-z-2-

Question Number 120593 by snipers237 last updated on 01/Nov/20

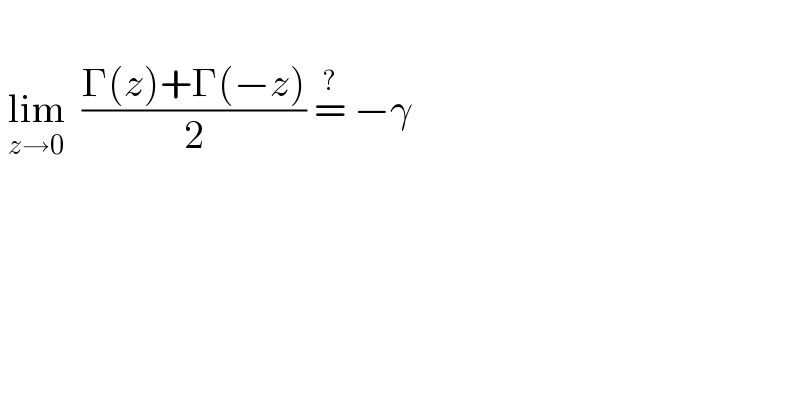
$$ \\ $$$$\:\underset{{z}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\frac{\Gamma\left({z}\right)+\Gamma\left(−{z}\right)}{\mathrm{2}}\:\overset{?} {=}\:−\gamma \\ $$

Answered by mnjuly1970 last updated on 02/Nov/20

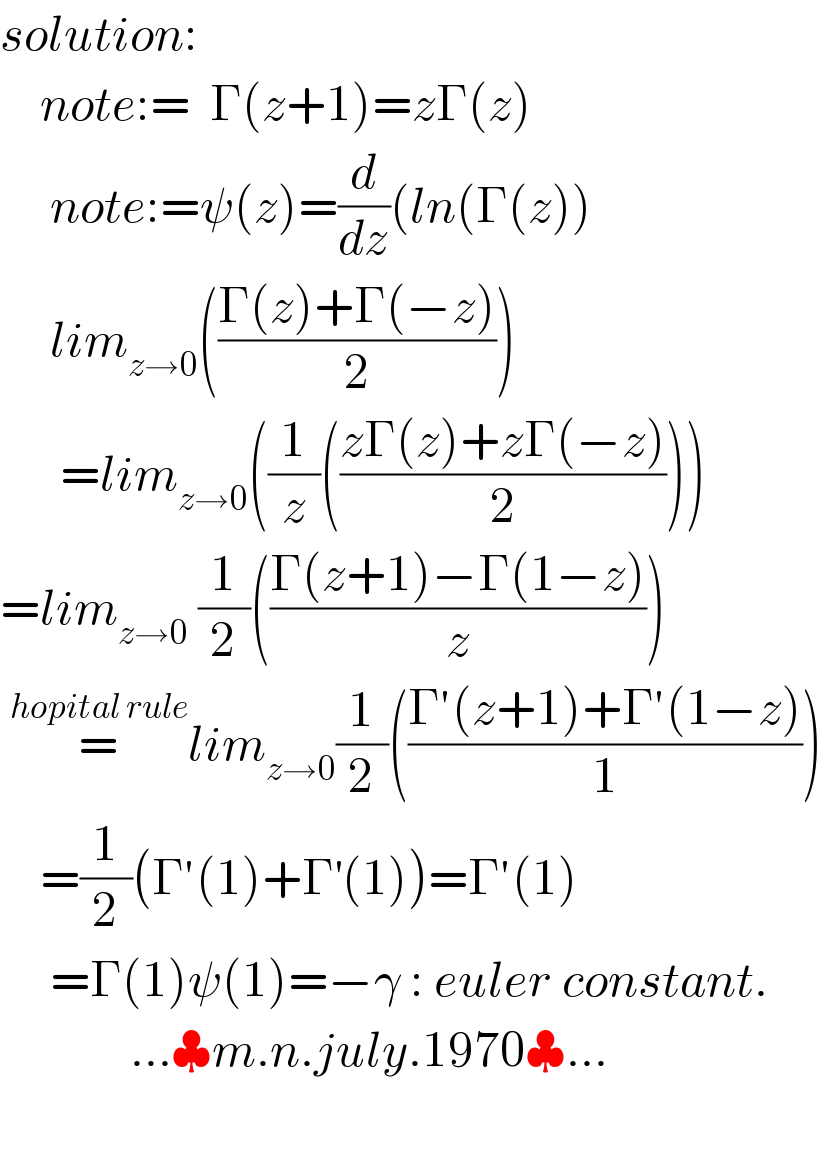
solution: note:= Γ(z+1)=zΓ(z) note:=ψ(z)=(d/dz)(ln(Γ(z)) lim_(z→0) (((Γ(z)+Γ(−z))/2)) =lim_(z→0) ((1/z)(((zΓ(z)+zΓ(−z))/2))) =lim_(z→0) (1/2)(((Γ(z+1)−Γ(1−z))/z)) =^(hopital rule) lim_(z→0) (1/2)(((Γ′(z+1)+Γ′(1−z))/1)) =(1/2)(Γ′(1)+Γ^′ (1))=Γ′(1) =Γ(1)ψ(1)=−γ : euler constant. ...♣m.n.july.1970♣...

$${solution}: \\ $$$$\:\:\:\:{note}:=\:\:\Gamma\left({z}+\mathrm{1}\right)={z}\Gamma\left({z}\right)\: \\ $$$$\:\:\:\:\:{note}:=\psi\left({z}\right)=\frac{{d}}{{dz}}\left({ln}\left(\Gamma\left({z}\right)\right)\right. \\ $$$$\:\:\:\:\:{lim}_{{z}\rightarrow\mathrm{0}} \left(\frac{\Gamma\left({z}\right)+\Gamma\left(−{z}\right)}{\mathrm{2}}\right) \\ $$$$\:\:\:\:\:\:={lim}_{{z}\rightarrow\mathrm{0}} \left(\frac{\mathrm{1}}{{z}}\left(\frac{{z}\Gamma\left({z}\right)+{z}\Gamma\left(−{z}\right)}{\mathrm{2}}\right)\right) \\ $$$$={lim}_{{z}\rightarrow\mathrm{0}} \:\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\Gamma\left({z}+\mathrm{1}\right)−\Gamma\left(\mathrm{1}−{z}\right)}{{z}}\right)\:\: \\ $$$$\:\overset{{hopital}\:{rule}} {=}{lim}_{{z}\rightarrow\mathrm{0}} \frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\Gamma'\left({z}+\mathrm{1}\right)+\Gamma'\left(\mathrm{1}−{z}\right)}{\mathrm{1}}\right) \\ $$$$\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\left(\Gamma'\left(\mathrm{1}\right)+\Gamma^{'} \left(\mathrm{1}\right)\right)=\Gamma'\left(\mathrm{1}\right) \\ $$$$\:\:\:\:\:=\Gamma\left(\mathrm{1}\right)\psi\left(\mathrm{1}\right)=−\gamma\::\:{euler}\:{constant}. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:…\clubsuit{m}.{n}.{july}.\mathrm{1970}\clubsuit… \\ $$$$ \\ $$

Commented by I want to learn more last updated on 02/Nov/20

$$\mathrm{Help}\:\mathrm{sir}. \\ $$

Commented by I want to learn more last updated on 02/Nov/20

Commented by Dwaipayan Shikari last updated on 03/Nov/20

∫(5x^4 +4x^3 −x^2 )^(−(1/2)) dx =∫(1/( (√(5x^4 +4x^3 −x^2 ))))dx =∫(1/(x(√(5x^2 +4x−1))))dx=∫(1/(x(√((5x−1)(x+1)))))dx =∫((1/x^2 )/( (√((5−(1/x))(1+(1/x))))))dx t=1+(1/x) =−∫(dt/( (√(t(6−t))))) =−∫(dt/( (√(9−(t−3)^2 )))) t−3=3sin𝛉⇒1=3cos𝛉(d𝛉/dt) =−∫((3cos𝛉d𝛉)/( (√(9−9sin^2 𝛉)))) =−∫d𝛉=−𝛉+C =−sin^(−1) (((t−3)/3))+C =−sin^(−1) (((1+(1/x)−3)/3))+c =−sin^(−1) (((−2x+1)/(3x)))+c

$$\int\left(\mathrm{5}{x}^{\mathrm{4}} +\mathrm{4}\boldsymbol{{x}}^{\mathrm{3}} −\boldsymbol{{x}}^{\mathrm{2}} \right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \boldsymbol{{dx}} \\ $$$$=\int\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}\boldsymbol{{x}}^{\mathrm{4}} +\mathrm{4}\boldsymbol{{x}}^{\mathrm{3}} −\boldsymbol{{x}}^{\mathrm{2}} }}\boldsymbol{{dx}} \\ $$$$=\int\frac{\mathrm{1}}{\boldsymbol{{x}}\sqrt{\mathrm{5}\boldsymbol{{x}}^{\mathrm{2}} +\mathrm{4}\boldsymbol{{x}}−\mathrm{1}}}\boldsymbol{{dx}}=\int\frac{\mathrm{1}}{\boldsymbol{{x}}\sqrt{\left(\mathrm{5}\boldsymbol{{x}}−\mathrm{1}\right)\left(\boldsymbol{{x}}+\mathrm{1}\right)}}\boldsymbol{{dx}} \\ $$$$=\int\frac{\frac{\mathrm{1}}{\boldsymbol{{x}}^{\mathrm{2}} }}{\:\sqrt{\left(\mathrm{5}−\frac{\mathrm{1}}{\boldsymbol{{x}}}\right)\left(\mathrm{1}+\frac{\mathrm{1}}{\boldsymbol{{x}}}\right)}}\boldsymbol{{dx}}\:\:\:\:\boldsymbol{{t}}=\mathrm{1}+\frac{\mathrm{1}}{\boldsymbol{{x}}} \\ $$$$=−\int\frac{\boldsymbol{{dt}}}{\:\sqrt{\boldsymbol{{t}}\left(\mathrm{6}−\boldsymbol{{t}}\right)}} \\ $$$$=−\int\frac{\boldsymbol{{dt}}}{\:\sqrt{\mathrm{9}−\left(\boldsymbol{{t}}−\mathrm{3}\right)^{\mathrm{2}} }}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{{t}}−\mathrm{3}=\mathrm{3}\boldsymbol{{sin}\theta}\Rightarrow\mathrm{1}=\mathrm{3}\boldsymbol{{cos}\theta}\frac{\boldsymbol{{d}\theta}}{\boldsymbol{{dt}}} \\ $$$$=−\int\frac{\mathrm{3}\boldsymbol{{cos}\theta}{d}\boldsymbol{\theta}}{\:\sqrt{\mathrm{9}−\mathrm{9}\boldsymbol{{sin}}^{\mathrm{2}} \boldsymbol{\theta}}} \\ $$$$=−\int\boldsymbol{{d}\theta}=−\boldsymbol{\theta}+{C} \\ $$$$=−\boldsymbol{{sin}}^{−\mathrm{1}} \left(\frac{\boldsymbol{{t}}−\mathrm{3}}{\mathrm{3}}\right)+\boldsymbol{{C}} \\ $$$$=−\boldsymbol{{sin}}^{−\mathrm{1}} \left(\frac{\mathrm{1}+\frac{\mathrm{1}}{\boldsymbol{{x}}}−\mathrm{3}}{\mathrm{3}}\right)+\boldsymbol{{c}} \\ $$$$=−\boldsymbol{{sin}}^{−\mathrm{1}} \left(\frac{−\mathrm{2}\boldsymbol{{x}}+\mathrm{1}}{\mathrm{3}\boldsymbol{{x}}}\right)+\boldsymbol{{c}} \\ $$

Commented by I want to learn more last updated on 03/Nov/20