Question Number 103314 by Ar Brandon last updated on 14/Jul/20
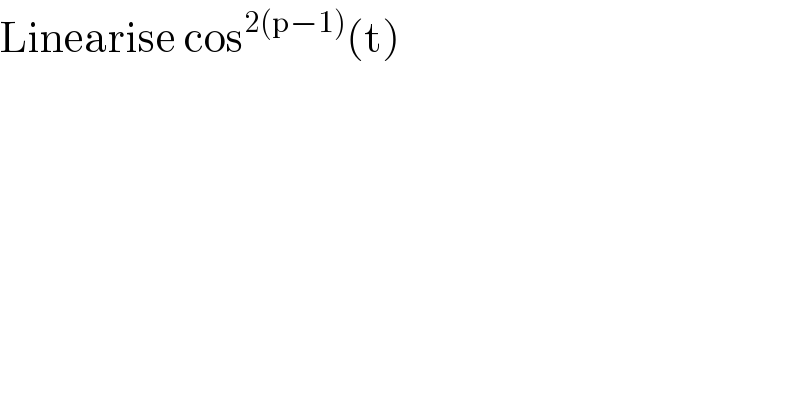
$$\mathrm{Linearise}\:\mathrm{cos}^{\mathrm{2}\left(\mathrm{p}−\mathrm{1}\right)} \left(\mathrm{t}\right) \\ $$
Answered by OlafThorendsen last updated on 14/Jul/20
![cos^(2(p−1)) (t) = [((e^(it) +e^(−it) )/2)]^(2(p−1)) cos^(2(p−1)) (t) = (1/4^(p−1) )Σ_(k=0) ^(2(p−1)) C_(2(p−1)) ^k e^(ikt) e^(−it(2p−2−k)) cos^(2(p−1)) (t) = (1/4^(p−1) )Σ_(k=0) ^(2(p−1)) C_(2(p−1)) ^k e^(−it(2p−2−2k)) cos^(2(p−1)) (t) = (1/4^(p−1) )Σ_(k=0) ^(2(p−1)) C_(2(p−1)) ^k e^(2it(k+1−p)) cos^(2(p−1)) (t) = (((2p−2)!)/4^(p−1) )Σ_(k=0) ^(2(p−1)) ((cos[2(k+1−p)t])/(k!(2p−2−k)!))](https://www.tinkutara.com/question/Q103316.png)
$$\mathrm{cos}^{\mathrm{2}\left({p}−\mathrm{1}\right)} \left({t}\right)\:=\:\left[\frac{{e}^{{it}} +{e}^{−{it}} }{\mathrm{2}}\right]^{\mathrm{2}\left({p}−\mathrm{1}\right)} \\ $$$$\mathrm{cos}^{\mathrm{2}\left({p}−\mathrm{1}\right)} \left({t}\right)\:=\:\frac{\mathrm{1}}{\mathrm{4}^{{p}−\mathrm{1}} }\underset{{k}=\mathrm{0}} {\overset{\mathrm{2}\left({p}−\mathrm{1}\right)} {\sum}}\mathrm{C}_{\mathrm{2}\left({p}−\mathrm{1}\right)} ^{{k}} {e}^{{ikt}} {e}^{−{it}\left(\mathrm{2}{p}−\mathrm{2}−{k}\right)} \\ $$$$\mathrm{cos}^{\mathrm{2}\left({p}−\mathrm{1}\right)} \left({t}\right)\:=\:\frac{\mathrm{1}}{\mathrm{4}^{{p}−\mathrm{1}} }\underset{{k}=\mathrm{0}} {\overset{\mathrm{2}\left({p}−\mathrm{1}\right)} {\sum}}\mathrm{C}_{\mathrm{2}\left({p}−\mathrm{1}\right)} ^{{k}} {e}^{−{it}\left(\mathrm{2}{p}−\mathrm{2}−\mathrm{2}{k}\right)} \\ $$$$\mathrm{cos}^{\mathrm{2}\left({p}−\mathrm{1}\right)} \left({t}\right)\:=\:\frac{\mathrm{1}}{\mathrm{4}^{{p}−\mathrm{1}} }\underset{{k}=\mathrm{0}} {\overset{\mathrm{2}\left({p}−\mathrm{1}\right)} {\sum}}\mathrm{C}_{\mathrm{2}\left({p}−\mathrm{1}\right)} ^{{k}} {e}^{\mathrm{2}{it}\left({k}+\mathrm{1}−{p}\right)} \\ $$$$\mathrm{cos}^{\mathrm{2}\left({p}−\mathrm{1}\right)} \left({t}\right)\:=\:\frac{\left(\mathrm{2}{p}−\mathrm{2}\right)!}{\mathrm{4}^{{p}−\mathrm{1}} }\underset{{k}=\mathrm{0}} {\overset{\mathrm{2}\left({p}−\mathrm{1}\right)} {\sum}}\frac{\mathrm{cos}\left[\mathrm{2}\left({k}+\mathrm{1}−{p}\right){t}\right]}{{k}!\left(\mathrm{2}{p}−\mathrm{2}−{k}\right)!} \\ $$$$ \\ $$
Commented by Ar Brandon last updated on 14/Jul/20

$$\mathcal{T}\mathrm{hanks} \\ $$
