Question Number 96705 by bemath last updated on 04/Jun/20
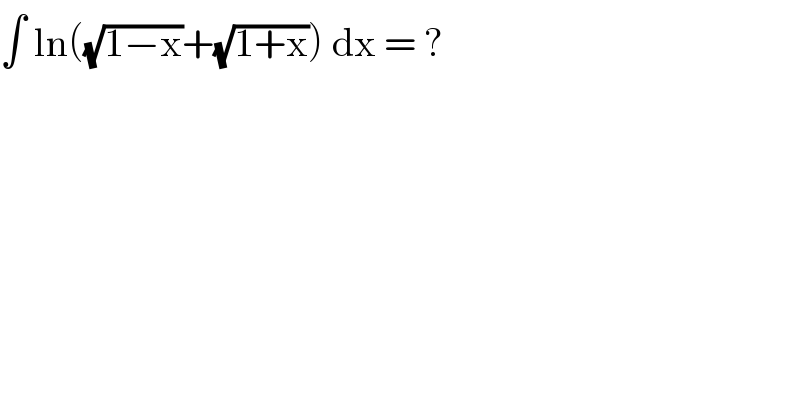
$$\int\:\mathrm{ln}\left(\sqrt{\mathrm{1}−\mathrm{x}}+\sqrt{\mathrm{1}+\mathrm{x}}\right)\:\mathrm{dx}\:=\:? \\ $$
Answered by john santu last updated on 04/Jun/20
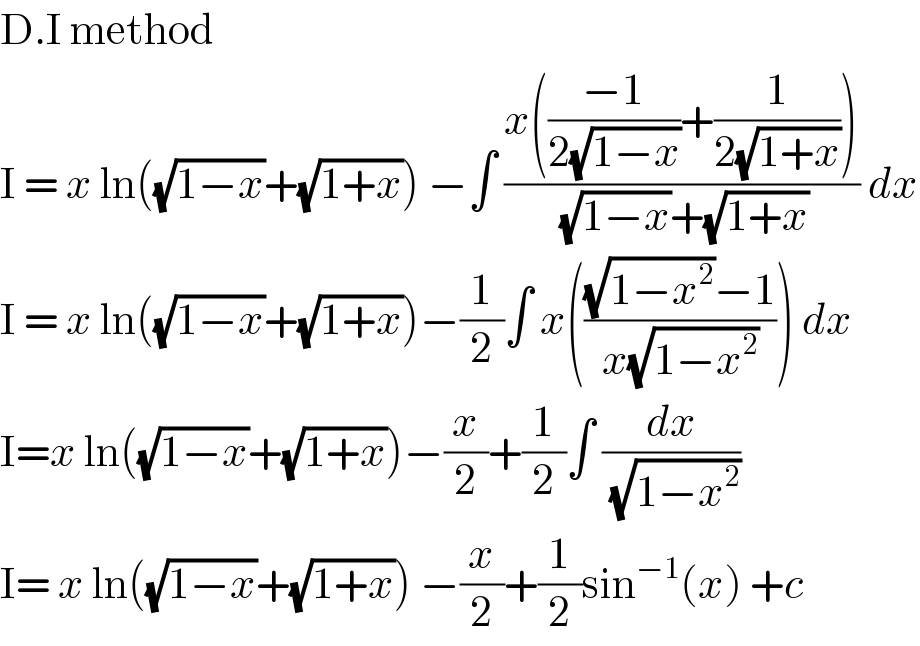
$$\mathrm{D}.\mathrm{I}\:\mathrm{method} \\ $$$$\mathrm{I}\:=\:{x}\:\mathrm{ln}\left(\sqrt{\mathrm{1}−{x}}+\sqrt{\mathrm{1}+{x}}\right)\:−\int\:\frac{{x}\left(\frac{−\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{1}−{x}}}+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{1}+{x}}}\right)}{\:\sqrt{\mathrm{1}−{x}}+\sqrt{\mathrm{1}+{x}}}\:{dx} \\ $$$$\mathrm{I}\:=\:{x}\:\mathrm{ln}\left(\sqrt{\mathrm{1}−{x}}+\sqrt{\mathrm{1}+{x}}\right)−\frac{\mathrm{1}}{\mathrm{2}}\int\:{x}\left(\frac{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }−\mathrm{1}}{{x}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\right)\:{dx} \\ $$$$\mathrm{I}={x}\:\mathrm{ln}\left(\sqrt{\mathrm{1}−{x}}+\sqrt{\mathrm{1}+{x}}\right)−\frac{{x}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{{dx}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }} \\ $$$$\mathrm{I}=\:{x}\:\mathrm{ln}\left(\sqrt{\mathrm{1}−{x}}+\sqrt{\mathrm{1}+{x}}\right)\:−\frac{{x}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}^{−\mathrm{1}} \left({x}\right)\:+{c}\: \\ $$
Commented by peter frank last updated on 04/Jun/20

$$\mathrm{thank}\:\mathrm{you} \\ $$
