ln-1-x-2-1-dx-

Question Number 105943 by bachamohamed last updated on 01/Aug/20

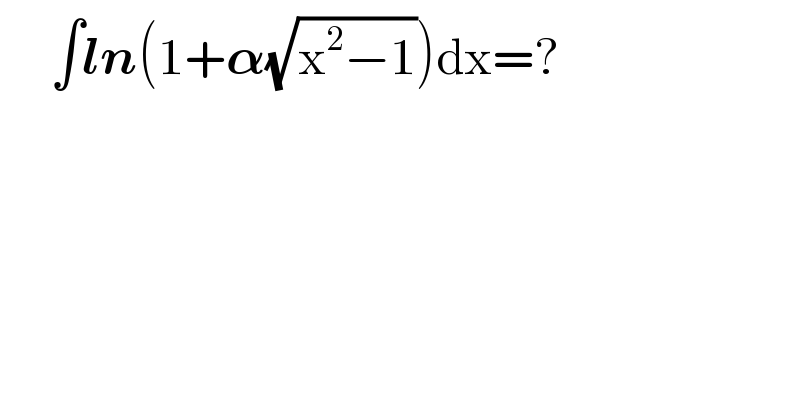
$$\:\:\:\:\:\int\boldsymbol{{ln}}\left(\mathrm{1}+\boldsymbol{\alpha}\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\right)\mathrm{dx}=? \\ $$

Answered by Dwaipayan Shikari last updated on 01/Aug/20

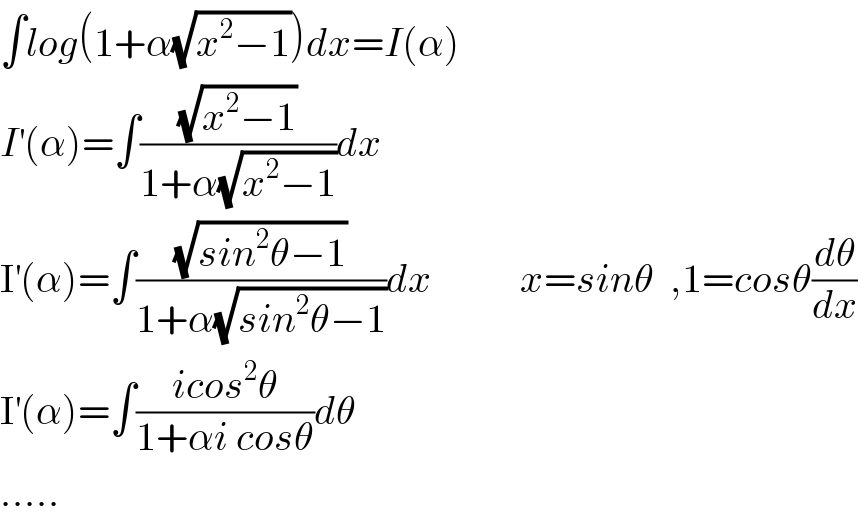
∫log(1+α(√(x^2 −1)))dx=I(α) I^′ (α)=∫((√(x^2 −1))/(1+α(√(x^2 −1))))dx I^′ (α)=∫((√(sin^2 θ−1))/(1+α(√(sin^2 θ−1))))dx x=sinθ ,1=cosθ(dθ/dx) I^′ (α)=∫((icos^2 θ)/(1+αi cosθ))dθ .....

$$\int{log}\left(\mathrm{1}+\alpha\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\right){dx}={I}\left(\alpha\right) \\ $$$${I}^{'} \left(\alpha\right)=\int\frac{\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}{\mathrm{1}+\alpha\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}{dx} \\ $$$$\mathrm{I}^{'} \left(\alpha\right)=\int\frac{\sqrt{{sin}^{\mathrm{2}} \theta−\mathrm{1}}}{\mathrm{1}+\alpha\sqrt{{sin}^{\mathrm{2}} \theta−\mathrm{1}}}{dx}\:\:\:\:\:\:\:\:\:\:\:{x}={sin}\theta\:\:,\mathrm{1}={cos}\theta\frac{{d}\theta}{{dx}} \\ $$$$\mathrm{I}^{'} \left(\alpha\right)=\int\frac{{icos}^{\mathrm{2}} \theta}{\mathrm{1}+\alpha{i}\:{cos}\theta}{d}\theta \\ $$$$….. \\ $$

Answered by mathmax by abdo last updated on 01/Aug/20

let f(t) =∫ln(1+t(√(x^2 −1)))dx ⇒ f^′ (t) =∫ ((√(x^2 −1))/(1+t(√(x^2 −1))))dx =(1/t)∫ ((1+t(√(x^2 −1))−1)/(1+t(√(x^2 −1))))dx =(x/t) −(1/t) ∫ (dx/(1+t(√(x^2 −1)))) we do the changement x =chu ⇒ ∫ (dx/(1+t(√(x^2 −1)))) =∫ ((shu du)/(1+t sh(u))) =∫ (((e^u −e^(−u) )/2)/(1+t((e^u −e^(−u) )/2))) du =∫ ((e^u −e^(−u) )/(2 +t e^u −t e^(−u) )) du =_(e^u =z) ∫ ((z−z^(−1) )/(2+tz−tz^(−1) ))(dz/z) =∫ ((z−z^(−1) )/(2z+tz^2 −t))dz =∫ ((z^2 −1)/(z(tz^2 +2z−t)))dz let decompose F(z) =((z^2 −1)/(z(tz^2 +2z−t))) tz^2 +2z−t =0→Δ^′ =1+t^2 ⇒ z_1 =((−1+(√(1+t^2 )))/t) and z_2 =((−1−(√(1+t^2 )))/t) F(z) =((z^2 −1)/(tz(z−z_1 )(z−z_2 ))) =((a(t))/z) +((b(t))/(z−z_1 )) +((c(t))/(z−z_2 )) a(t) =((−1)/(t(−1))) =(1/t) , b(t) =((z_1 ^2 −1)/(tz_1 (z_1 −z_2 ))) , c(t) =((z_2 ^2 −1)/(tz_2 (z_2 −z_1 ))) ⇒ ∫ (dx/(1+t(√(x^2 −1)))) =a(t)ln∣z∣ +b(t)ln∣z−z_1 ∣ +c(t)ln∣z−z_2 ∣ +c ⇒ ⇒f(t) =xln(t)−(1/t) (∫ a(t)ln∣z∣dt +∫ b(t)ln∣z−z_1 ∣ +∫c(t)ln∣z−z_2 ∣dt +c)

$$\mathrm{let}\:\mathrm{f}\left(\mathrm{t}\right)\:=\int\mathrm{ln}\left(\mathrm{1}+\mathrm{t}\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\right)\mathrm{dx}\:\Rightarrow \\ $$$$\mathrm{f}^{'} \left(\mathrm{t}\right)\:=\int\:\frac{\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}}{\mathrm{1}+\mathrm{t}\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}}\mathrm{dx}\:=\frac{\mathrm{1}}{\mathrm{t}}\int\:\frac{\mathrm{1}+\mathrm{t}\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}−\mathrm{1}}{\mathrm{1}+\mathrm{t}\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}}\mathrm{dx} \\ $$$$=\frac{\mathrm{x}}{\mathrm{t}}\:−\frac{\mathrm{1}}{\mathrm{t}}\:\int\:\frac{\mathrm{dx}}{\mathrm{1}+\mathrm{t}\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}}\:\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\mathrm{x}\:=\mathrm{chu}\:\Rightarrow \\ $$$$\int\:\frac{\mathrm{dx}}{\mathrm{1}+\mathrm{t}\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}}\:=\int\:\:\:\frac{\mathrm{shu}\:\mathrm{du}}{\mathrm{1}+\mathrm{t}\:\mathrm{sh}\left(\mathrm{u}\right)}\:=\int\:\:\frac{\frac{\mathrm{e}^{\mathrm{u}} −\mathrm{e}^{−\mathrm{u}} }{\mathrm{2}}}{\mathrm{1}+\mathrm{t}\frac{\mathrm{e}^{\mathrm{u}} −\mathrm{e}^{−\mathrm{u}} }{\mathrm{2}}}\:\mathrm{du} \\ $$$$=\int\:\:\:\frac{\mathrm{e}^{\mathrm{u}} −\mathrm{e}^{−\mathrm{u}} }{\mathrm{2}\:+\mathrm{t}\:\mathrm{e}^{\mathrm{u}} −\mathrm{t}\:\mathrm{e}^{−\mathrm{u}} }\:\mathrm{du}\:=_{\mathrm{e}^{\mathrm{u}} \:=\mathrm{z}} \:\:\:\int\:\:\frac{\mathrm{z}−\mathrm{z}^{−\mathrm{1}} }{\mathrm{2}+\mathrm{tz}−\mathrm{tz}^{−\mathrm{1}} }\frac{\mathrm{dz}}{\mathrm{z}} \\ $$$$=\int\:\:\frac{\mathrm{z}−\mathrm{z}^{−\mathrm{1}} }{\mathrm{2z}+\mathrm{tz}^{\mathrm{2}} −\mathrm{t}}\mathrm{dz}\:=\int\:\frac{\mathrm{z}^{\mathrm{2}} −\mathrm{1}}{\mathrm{z}\left(\mathrm{tz}^{\mathrm{2}} +\mathrm{2z}−\mathrm{t}\right)}\mathrm{dz}\:\:\mathrm{let}\:\mathrm{decompose}\: \\ $$$$\mathrm{F}\left(\mathrm{z}\right)\:=\frac{\mathrm{z}^{\mathrm{2}} −\mathrm{1}}{\mathrm{z}\left(\mathrm{tz}^{\mathrm{2}} +\mathrm{2z}−\mathrm{t}\right)} \\ $$$$\mathrm{tz}^{\mathrm{2}} \:+\mathrm{2z}−\mathrm{t}\:=\mathrm{0}\rightarrow\Delta^{'} \:=\mathrm{1}+\mathrm{t}^{\mathrm{2}} \:\Rightarrow\:\mathrm{z}_{\mathrm{1}} =\frac{−\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }}{\mathrm{t}}\:\mathrm{and}\:\mathrm{z}_{\mathrm{2}} =\frac{−\mathrm{1}−\sqrt{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }}{\mathrm{t}} \\ $$$$\mathrm{F}\left(\mathrm{z}\right)\:=\frac{\mathrm{z}^{\mathrm{2}} −\mathrm{1}}{\mathrm{tz}\left(\mathrm{z}−\mathrm{z}_{\mathrm{1}} \right)\left(\mathrm{z}−\mathrm{z}_{\mathrm{2}} \right)}\:=\frac{\mathrm{a}\left(\mathrm{t}\right)}{\mathrm{z}}\:+\frac{\mathrm{b}\left(\mathrm{t}\right)}{\mathrm{z}−\mathrm{z}_{\mathrm{1}} }\:+\frac{\mathrm{c}\left(\mathrm{t}\right)}{\mathrm{z}−\mathrm{z}_{\mathrm{2}} } \\ $$$$\mathrm{a}\left(\mathrm{t}\right)\:=\frac{−\mathrm{1}}{\mathrm{t}\left(−\mathrm{1}\right)}\:=\frac{\mathrm{1}}{\mathrm{t}}\:,\:\mathrm{b}\left(\mathrm{t}\right)\:=\frac{\mathrm{z}_{\mathrm{1}} ^{\mathrm{2}} −\mathrm{1}}{\mathrm{tz}_{\mathrm{1}} \left(\mathrm{z}_{\mathrm{1}} −\mathrm{z}_{\mathrm{2}} \right)}\:,\:\:\mathrm{c}\left(\mathrm{t}\right)\:=\frac{\mathrm{z}_{\mathrm{2}} ^{\mathrm{2}} −\mathrm{1}}{\mathrm{tz}_{\mathrm{2}} \left(\mathrm{z}_{\mathrm{2}} −\mathrm{z}_{\mathrm{1}} \right)}\:\Rightarrow \\ $$$$\int\:\:\frac{\mathrm{dx}}{\mathrm{1}+\mathrm{t}\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}}\:=\mathrm{a}\left(\mathrm{t}\right)\mathrm{ln}\mid\mathrm{z}\mid\:+\mathrm{b}\left(\mathrm{t}\right)\mathrm{ln}\mid\mathrm{z}−\mathrm{z}_{\mathrm{1}} \mid\:+\mathrm{c}\left(\mathrm{t}\right)\mathrm{ln}\mid\mathrm{z}−\mathrm{z}_{\mathrm{2}} \mid\:+\mathrm{c}\:\Rightarrow \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{t}\right)\:=\mathrm{xln}\left(\mathrm{t}\right)−\frac{\mathrm{1}}{\mathrm{t}}\:\left(\int\:\mathrm{a}\left(\mathrm{t}\right)\mathrm{ln}\mid\mathrm{z}\mid\mathrm{dt}\:+\int\:\mathrm{b}\left(\mathrm{t}\right)\mathrm{ln}\mid\mathrm{z}−\mathrm{z}_{\mathrm{1}} \mid\:+\int\mathrm{c}\left(\mathrm{t}\right)\mathrm{ln}\mid\mathrm{z}−\mathrm{z}_{\mathrm{2}} \mid\mathrm{dt}\:+\mathrm{c}\right) \\ $$

Answered by mathmax by abdo last updated on 01/Aug/20

another way by parys I =xln(1+α(√(x^2 −1)))−∫ x×((αx)/( (√(x^2 −1))(1+α(√(x^2 −1)))))dx =xln(1+α(√(x^2 −1))) −α ∫ (x^2 /( (√(x^2 −1))(1+α(√(x^2 −1)))))dx changement x =ch(t) give ∫ (x^2 /( (√(x^2 −1))(1+α(√(x^2 −1)))))dx =∫ ((ch^2 (t))/(sh(t)(1+α sht)))sh(t)dt =∫ ((ch^2 (t))/(1+α sh(t)))dt =(1/2)∫ ((1+ch(2t))/(1+αsh(t)dt))dt =(1/2)∫ ((1+((e^(2t) +e^(−2t) )/2))/(1+α((e^t −e^(−t) )/2))) dt =(1/2)∫ ((2+e^(2t) +e^(−2t) )/(2+αe^t −αe^(−t) ))dt =_(e^t =u) (1/2) ∫((2+u^2 +u^(−2) )/(2+αu−αu^(−1) ))(du/u) =(1/2)∫ ((2+u^2 +u^(−2) )/(2u+αu^2 −α)) du =(1/2)∫ ((2u^2 +u^4 +1)/(u^2 (αu^2 +2u−α)))du let decompose F(u) =((u^4 +2u^2 +1)/(u^2 (αu^2 +2u−α))) ⇒F(u) =((u^4 +2u^2 +1)/(αu^4 +2u^3 −αu^2 )) =(1/α)((αu^4 +2αu^2 +α)/(αu^4 +2u^3 −αu^2 )) =(1/α)×((αu^4 +2u^3 −αu^2 −2u^3 +αu^2 +2αu^2 +α)/((...)))

$$\mathrm{another}\:\mathrm{way}\:\mathrm{by}\:\mathrm{parys}\: \\ $$$$\mathrm{I}\:=\mathrm{xln}\left(\mathrm{1}+\alpha\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\right)−\int\:\:\mathrm{x}×\frac{\alpha\mathrm{x}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\left(\mathrm{1}+\alpha\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\right)}\mathrm{dx} \\ $$$$=\mathrm{xln}\left(\mathrm{1}+\alpha\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\right)\:−\alpha\:\int\:\:\frac{\mathrm{x}^{\mathrm{2}} }{\:\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\left(\mathrm{1}+\alpha\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\right)}\mathrm{dx} \\ $$$$\mathrm{changement}\:\mathrm{x}\:=\mathrm{ch}\left(\mathrm{t}\right)\:\mathrm{give}\: \\ $$$$\int\:\frac{\mathrm{x}^{\mathrm{2}} }{\:\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\left(\mathrm{1}+\alpha\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\right)}\mathrm{dx}\:=\int\:\frac{\mathrm{ch}^{\mathrm{2}} \left(\mathrm{t}\right)}{\mathrm{sh}\left(\mathrm{t}\right)\left(\mathrm{1}+\alpha\:\mathrm{sht}\right)}\mathrm{sh}\left(\mathrm{t}\right)\mathrm{dt} \\ $$$$=\int\:\:\frac{\mathrm{ch}^{\mathrm{2}} \left(\mathrm{t}\right)}{\mathrm{1}+\alpha\:\mathrm{sh}\left(\mathrm{t}\right)}\mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{2}}\int\:\:\frac{\mathrm{1}+\mathrm{ch}\left(\mathrm{2t}\right)}{\mathrm{1}+\alpha\mathrm{sh}\left(\mathrm{t}\right)\mathrm{dt}}\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\:\:\frac{\mathrm{1}+\frac{\mathrm{e}^{\mathrm{2t}} +\mathrm{e}^{−\mathrm{2t}} }{\mathrm{2}}}{\mathrm{1}+\alpha\frac{\mathrm{e}^{\mathrm{t}} −\mathrm{e}^{−\mathrm{t}} }{\mathrm{2}}}\:\mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\mathrm{2}+\mathrm{e}^{\mathrm{2t}} \:+\mathrm{e}^{−\mathrm{2t}} }{\mathrm{2}+\alpha\mathrm{e}^{\mathrm{t}} −\alpha\mathrm{e}^{−\mathrm{t}} }\mathrm{dt} \\ $$$$=_{\mathrm{e}^{\mathrm{t}} \:=\mathrm{u}} \:\:\:\:\frac{\mathrm{1}}{\mathrm{2}}\:\int\frac{\mathrm{2}+\mathrm{u}^{\mathrm{2}} \:+\mathrm{u}^{−\mathrm{2}} }{\mathrm{2}+\alpha\mathrm{u}−\alpha\mathrm{u}^{−\mathrm{1}} }\frac{\mathrm{du}}{\mathrm{u}}\:=\frac{\mathrm{1}}{\mathrm{2}}\int\:\:\frac{\mathrm{2}+\mathrm{u}^{\mathrm{2}} +\mathrm{u}^{−\mathrm{2}} }{\mathrm{2u}+\alpha\mathrm{u}^{\mathrm{2}} −\alpha}\:\mathrm{du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\mathrm{2u}^{\mathrm{2}} \:+\mathrm{u}^{\mathrm{4}} \:+\mathrm{1}}{\mathrm{u}^{\mathrm{2}} \left(\alpha\mathrm{u}^{\mathrm{2}} +\mathrm{2u}−\alpha\right)}\mathrm{du}\:\:\mathrm{let}\:\mathrm{decompose}\: \\ $$$$\mathrm{F}\left(\mathrm{u}\right)\:=\frac{\mathrm{u}^{\mathrm{4}} \:+\mathrm{2u}^{\mathrm{2}} \:+\mathrm{1}}{\mathrm{u}^{\mathrm{2}} \left(\alpha\mathrm{u}^{\mathrm{2}} \:+\mathrm{2u}−\alpha\right)}\:\Rightarrow\mathrm{F}\left(\mathrm{u}\right)\:=\frac{\mathrm{u}^{\mathrm{4}} \:+\mathrm{2u}^{\mathrm{2}} \:+\mathrm{1}}{\alpha\mathrm{u}^{\mathrm{4}} \:+\mathrm{2u}^{\mathrm{3}} \:−\alpha\mathrm{u}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\alpha}\frac{\alpha\mathrm{u}^{\mathrm{4}} \:+\mathrm{2}\alpha\mathrm{u}^{\mathrm{2}} \:+\alpha}{\alpha\mathrm{u}^{\mathrm{4}} \:+\mathrm{2u}^{\mathrm{3}} −\alpha\mathrm{u}^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\alpha}×\frac{\alpha\mathrm{u}^{\mathrm{4}} \:+\mathrm{2u}^{\mathrm{3}} −\alpha\mathrm{u}^{\mathrm{2}} −\mathrm{2u}^{\mathrm{3}} +\alpha\mathrm{u}^{\mathrm{2}} +\mathrm{2}\alpha\mathrm{u}^{\mathrm{2}} +\alpha}{\left(…\right)} \\ $$$$ \\ $$

Commented by mathmax by abdo last updated on 01/Aug/20

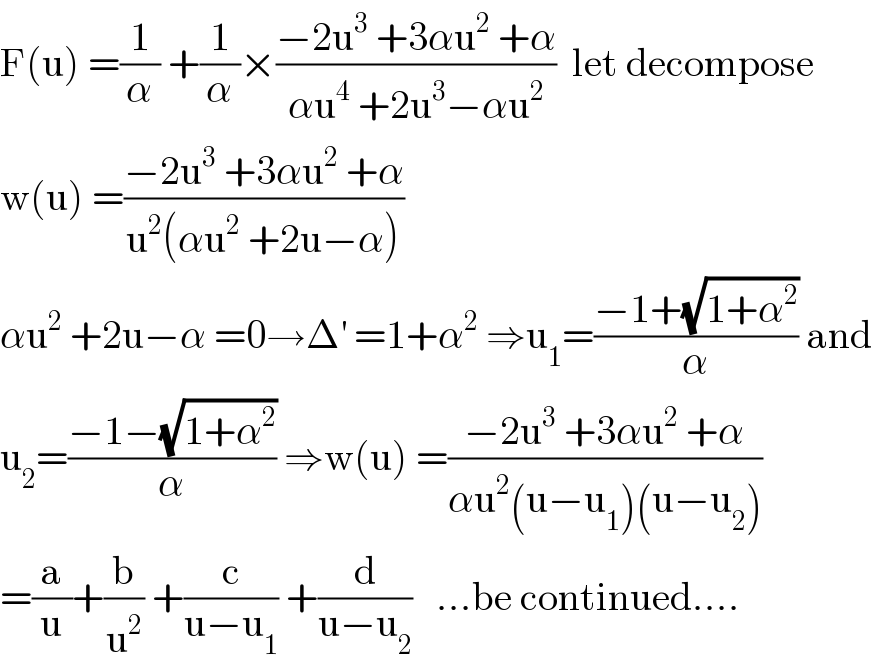
F(u) =(1/α) +(1/α)×((−2u^3 +3αu^2 +α)/(αu^4 +2u^3 −αu^2 )) let decompose w(u) =((−2u^3 +3αu^2 +α)/(u^2 (αu^2 +2u−α))) αu^2 +2u−α =0→Δ^′ =1+α^2 ⇒u_1 =((−1+(√(1+α^2 )))/α) and u_2 =((−1−(√(1+α^2 )))/α) ⇒w(u) =((−2u^3 +3αu^2 +α)/(αu^2 (u−u_1 )(u−u_2 ))) =(a/u)+(b/u^2 ) +(c/(u−u_1 )) +(d/(u−u_2 )) ...be continued....

$$\mathrm{F}\left(\mathrm{u}\right)\:=\frac{\mathrm{1}}{\alpha}\:+\frac{\mathrm{1}}{\alpha}×\frac{−\mathrm{2u}^{\mathrm{3}} \:+\mathrm{3}\alpha\mathrm{u}^{\mathrm{2}} \:+\alpha}{\alpha\mathrm{u}^{\mathrm{4}} \:+\mathrm{2u}^{\mathrm{3}} −\alpha\mathrm{u}^{\mathrm{2}} }\:\:\mathrm{let}\:\mathrm{decompose}\: \\ $$$$\mathrm{w}\left(\mathrm{u}\right)\:=\frac{−\mathrm{2u}^{\mathrm{3}} \:+\mathrm{3}\alpha\mathrm{u}^{\mathrm{2}} \:+\alpha}{\mathrm{u}^{\mathrm{2}} \left(\alpha\mathrm{u}^{\mathrm{2}} \:+\mathrm{2u}−\alpha\right)} \\ $$$$\alpha\mathrm{u}^{\mathrm{2}} \:+\mathrm{2u}−\alpha\:=\mathrm{0}\rightarrow\Delta^{'} \:=\mathrm{1}+\alpha^{\mathrm{2}} \:\Rightarrow\mathrm{u}_{\mathrm{1}} =\frac{−\mathrm{1}+\sqrt{\mathrm{1}+\alpha^{\mathrm{2}} }}{\alpha}\:\mathrm{and} \\ $$$$\mathrm{u}_{\mathrm{2}} =\frac{−\mathrm{1}−\sqrt{\mathrm{1}+\alpha^{\mathrm{2}} }}{\alpha}\:\Rightarrow\mathrm{w}\left(\mathrm{u}\right)\:=\frac{−\mathrm{2u}^{\mathrm{3}} \:+\mathrm{3}\alpha\mathrm{u}^{\mathrm{2}} \:+\alpha}{\alpha\mathrm{u}^{\mathrm{2}} \left(\mathrm{u}−\mathrm{u}_{\mathrm{1}} \right)\left(\mathrm{u}−\mathrm{u}_{\mathrm{2}} \right)} \\ $$$$=\frac{\mathrm{a}}{\mathrm{u}}+\frac{\mathrm{b}}{\mathrm{u}^{\mathrm{2}} }\:+\frac{\mathrm{c}}{\mathrm{u}−\mathrm{u}_{\mathrm{1}} }\:+\frac{\mathrm{d}}{\mathrm{u}−\mathrm{u}_{\mathrm{2}} }\:\:\:…\mathrm{be}\:\mathrm{continued}…. \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply