Question Number 146959 by Gbenga last updated on 16/Jul/21
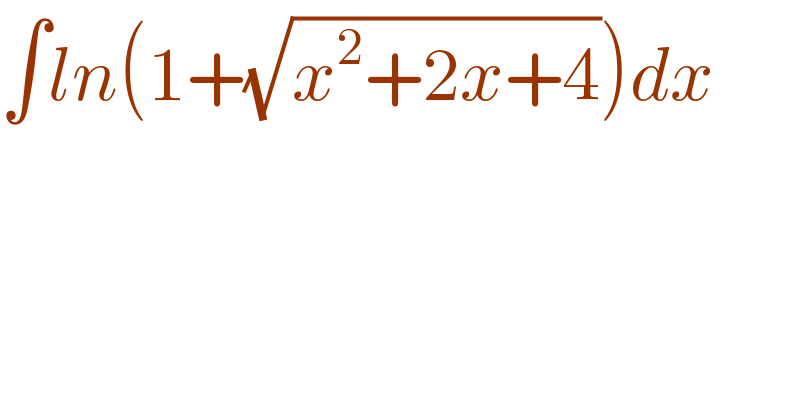
$$\int{ln}\left(\mathrm{1}+\sqrt{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{4}}\right){dx} \\ $$
Answered by mindispower last updated on 17/Jul/21
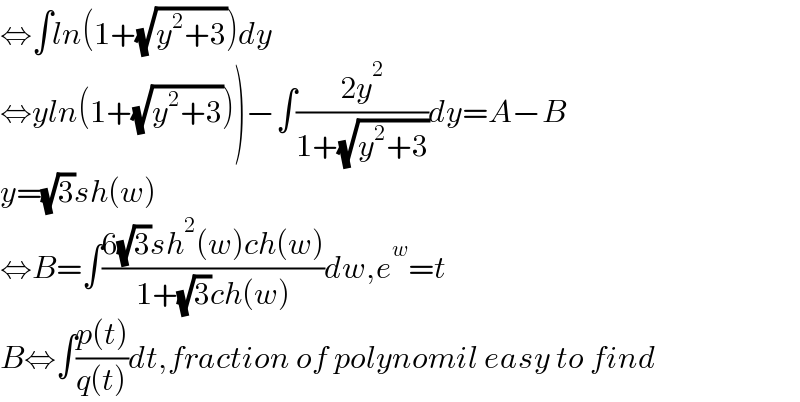
$$\Leftrightarrow\int{ln}\left(\mathrm{1}+\sqrt{{y}^{\mathrm{2}} +\mathrm{3}}\right){dy} \\ $$$$\left.\Leftrightarrow{yln}\left(\mathrm{1}+\sqrt{{y}^{\mathrm{2}} +\mathrm{3}}\right)\right)−\int\frac{\mathrm{2}{y}^{\mathrm{2}} }{\mathrm{1}+\sqrt{{y}^{\mathrm{2}} +\mathrm{3}}}{dy}={A}−{B} \\ $$$${y}=\sqrt{\mathrm{3}}{sh}\left({w}\right) \\ $$$$\Leftrightarrow{B}=\int\frac{\mathrm{6}\sqrt{\mathrm{3}}{sh}^{\mathrm{2}} \left({w}\right){ch}\left({w}\right)}{\mathrm{1}+\sqrt{\mathrm{3}}{ch}\left({w}\right)}{dw},{e}^{{w}} ={t} \\ $$$${B}\Leftrightarrow\int\frac{{p}\left({t}\right)}{{q}\left({t}\right)}{dt},{fraction}\:{of}\:{polynomil}\:{easy}\:{to}\:{find} \\ $$
Commented by Gbenga last updated on 17/Jul/21
$${thanks}\:{sir}\: \\ $$
