Question Number 114403 by bemath last updated on 19/Sep/20
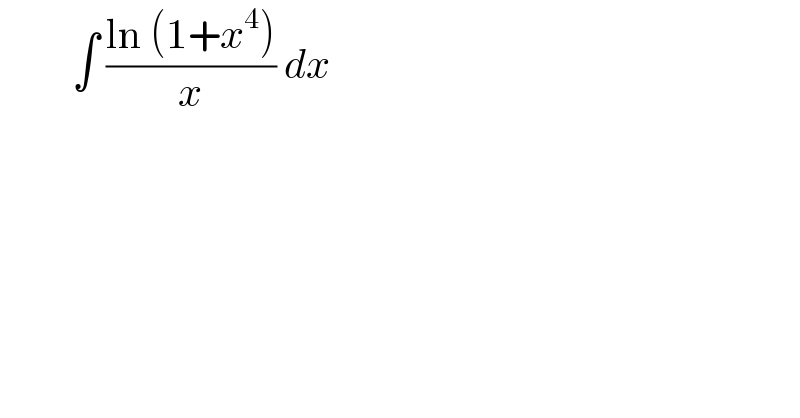
$$\:\:\:\:\:\:\:\:\:\int\:\frac{\mathrm{ln}\:\left(\mathrm{1}+{x}^{\mathrm{4}} \right)}{{x}}\:{dx} \\ $$$$ \\ $$
Commented by Dwaipayan Shikari last updated on 19/Sep/20
![∫_0 ^1 (−1)^n .Σ_(n=1) ^∞ (x^(4n−1) /n)dx Σ_(n=1) ^∞ (−1)^n ∫_0 ^1 (x^(4n−1) /n)dx Σ^∞ (−1)^n [(x^(4n) /(4n.n))]_0 ^1 (1/4)Σ^∞ (−1)^n (1/n^2 )=(π^2 /(48))](https://www.tinkutara.com/question/Q114492.png)
$$\int_{\mathrm{0}} ^{\mathrm{1}} \left(−\mathrm{1}\right)^{{n}} .\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{x}^{\mathrm{4}{n}−\mathrm{1}} }{{n}}{dx} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{4}{n}−\mathrm{1}} }{{n}}{dx} \\ $$$$\overset{\infty} {\sum}\left(−\mathrm{1}\right)^{{n}} \left[\frac{{x}^{\mathrm{4}{n}} }{\mathrm{4}{n}.{n}}\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\overset{\infty} {\sum}\left(−\mathrm{1}\right)^{{n}} \frac{\mathrm{1}}{{n}^{\mathrm{2}} }=\frac{\pi^{\mathrm{2}} }{\mathrm{48}} \\ $$
Answered by mathmax by abdo last updated on 19/Sep/20

$$\mathrm{if}\:\mathrm{the}\:\mathrm{Q}\:\mathrm{is}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{4}} \right)}{\mathrm{x}}\:\mathrm{dx}\:\:\mathrm{we}\:\mathrm{have}\:\frac{\mathrm{d}}{\mathrm{du}}\mathrm{ln}\left(\mathrm{1}+\mathrm{u}\right)\:=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{u}}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{u}^{\mathrm{n}} \\ $$$$\Rightarrow\mathrm{ln}\left(\mathrm{1}+\mathrm{u}\right)\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}} \:\frac{\mathrm{u}^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}+\mathrm{1}}\:+\mathrm{c}\left(\mathrm{c}=\mathrm{0}\right)\:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} \:\frac{\mathrm{u}^{\mathrm{n}} }{\mathrm{n}} \\ $$$$\Rightarrow\mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{4}} \right)\:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} \:\frac{\mathrm{x}^{\mathrm{4n}} }{\mathrm{n}}\:\Rightarrow\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{4}} \right)}{\mathrm{x}}\:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}}\:\mathrm{x}^{\mathrm{4n}−\mathrm{1}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{4}} \right)}{\mathrm{x}}\mathrm{dx}\:\:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{4n}−\mathrm{1}} \:\mathrm{dx} \\ $$$$=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}}×\frac{\mathrm{1}}{\mathrm{4n}}\:=−\frac{\mathrm{1}}{\mathrm{4}}\:\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}^{\mathrm{2}} } \\ $$$$=−\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{2}^{\mathrm{1}−\mathrm{2}} −\mathrm{1}\right)\xi\left(\mathrm{2}\right)\:=−\frac{\mathrm{1}}{\mathrm{4}}×\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)×\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:=\frac{\pi^{\mathrm{2}} }{\mathrm{48}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{4}} \right)}{\mathrm{x}}\mathrm{dx}\:=\frac{\pi^{\mathrm{2}} }{\mathrm{48}} \\ $$
