Menu Close

ln-cht-dt-

Tinku Tara 0 Comments
Pin




Question Number 146996 by ArielVyny last updated on 17/Jul/21
∫ln(cht)dt
$$\int{ln}\left({cht}\right){dt} \\ $$
Answered by mathmax by abdo last updated on 17/Jul/21
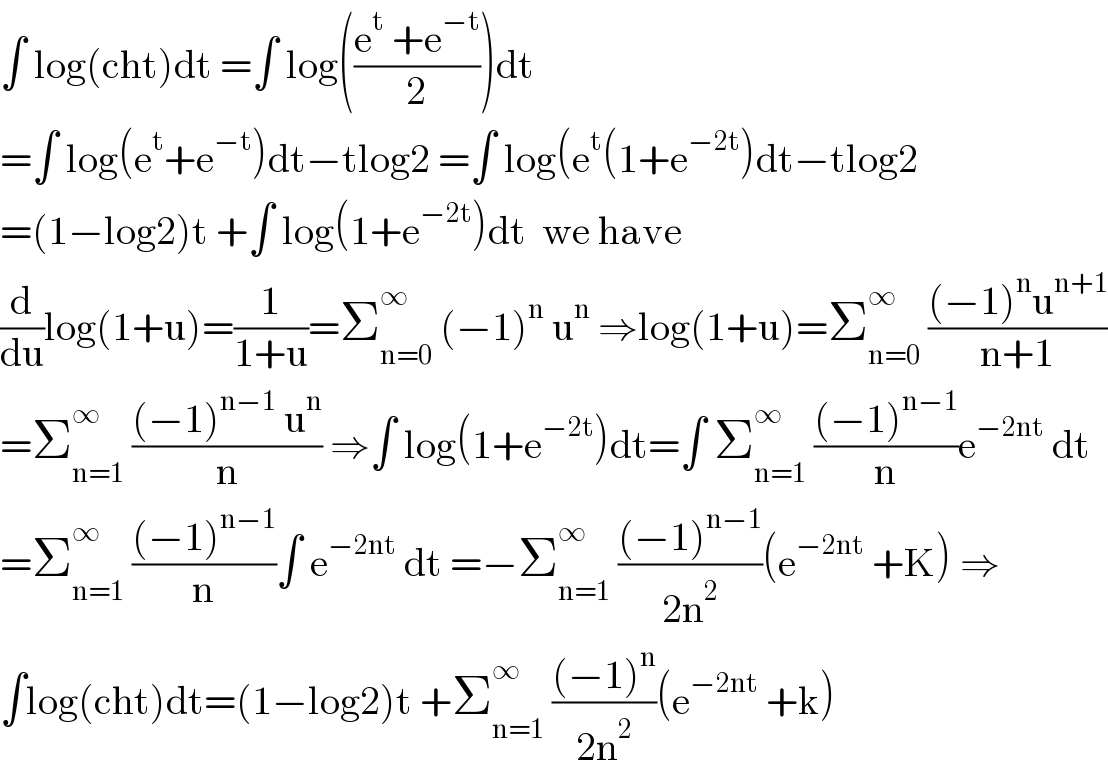
∫ log(cht)dt =∫ log(((e^t +e^(−t) )/2))dt =∫ log(e^t +e^(−t) )dt−tlog2 =∫ log(e^t (1+e^(−2t) )dt−tlog2 =(1−log2)t +∫ log(1+e^(−2t) )dt we have (d/du)log(1+u)=(1/(1+u))=Σ_(n=0) ^∞ (−1)^n u^n ⇒log(1+u)=Σ_(n=0) ^∞ (((−1)^n u^(n+1) )/(n+1)) =Σ_(n=1) ^∞ (((−1)^(n−1) u^n )/n) ⇒∫ log(1+e^(−2t) )dt=∫ Σ_(n=1) ^∞ (((−1)^(n−1) )/n)e^(−2nt) dt =Σ_(n=1) ^∞ (((−1)^(n−1) )/n)∫ e^(−2nt) dt =−Σ_(n=1) ^∞ (((−1)^(n−1) )/(2n^2 ))(e^(−2nt) +K) ⇒ ∫log(cht)dt=(1−log2)t +Σ_(n=1) ^∞ (((−1)^n )/(2n^2 ))(e^(−2nt) +k)
$$\int\:\mathrm{log}\left(\mathrm{cht}\right)\mathrm{dt}\:=\int\:\mathrm{log}\left(\frac{\mathrm{e}^{\mathrm{t}} \:+\mathrm{e}^{−\mathrm{t}} }{\mathrm{2}}\right)\mathrm{dt} \\ $$$$=\int\:\mathrm{log}\left(\mathrm{e}^{\mathrm{t}} +\mathrm{e}^{−\mathrm{t}} \right)\mathrm{dt}−\mathrm{tlog2}\:=\int\:\mathrm{log}\left(\mathrm{e}^{\mathrm{t}} \left(\mathrm{1}+\mathrm{e}^{−\mathrm{2t}} \right)\mathrm{dt}−\mathrm{tlog2}\right. \\ $$$$=\left(\mathrm{1}−\mathrm{log2}\right)\mathrm{t}\:+\int\:\mathrm{log}\left(\mathrm{1}+\mathrm{e}^{−\mathrm{2t}} \right)\mathrm{dt}\:\:\mathrm{we}\:\mathrm{have} \\ $$$$\frac{\mathrm{d}}{\mathrm{du}}\mathrm{log}\left(\mathrm{1}+\mathrm{u}\right)=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{u}}=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{u}^{\mathrm{n}} \:\Rightarrow\mathrm{log}\left(\mathrm{1}+\mathrm{u}\right)=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \mathrm{u}^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}+\mathrm{1}} \\ $$$$=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} \:\mathrm{u}^{\mathrm{n}} }{\mathrm{n}}\:\Rightarrow\int\:\mathrm{log}\left(\mathrm{1}+\mathrm{e}^{−\mathrm{2t}} \right)\mathrm{dt}=\int\:\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}}\mathrm{e}^{−\mathrm{2nt}} \:\mathrm{dt} \\ $$$$=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}}\int\:\mathrm{e}^{−\mathrm{2nt}} \:\mathrm{dt}\:=−\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\mathrm{2n}^{\mathrm{2}} }\left(\mathrm{e}^{−\mathrm{2nt}} \:+\mathrm{K}\right)\:\Rightarrow \\ $$$$\int\mathrm{log}\left(\mathrm{cht}\right)\mathrm{dt}=\left(\mathrm{1}−\mathrm{log2}\right)\mathrm{t}\:+\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{2n}^{\mathrm{2}} }\left(\mathrm{e}^{−\mathrm{2nt}} \:+\mathrm{k}\right) \\ $$
Commented by ArielVyny last updated on 17/Jul/21
thank mr
$${thank}\:{mr} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *