Question Number 151486 by mathocean1 last updated on 21/Aug/21

$$\int{ln}\left({sinx}\right)=?\: \\ $$$${x}\:\neq\:\mathrm{0}\:+\:\mathrm{2}{k}\pi\:;\:{k}\:\in\:\mathbb{Z} \\ $$
Answered by Olaf_Thorendsen last updated on 21/Aug/21
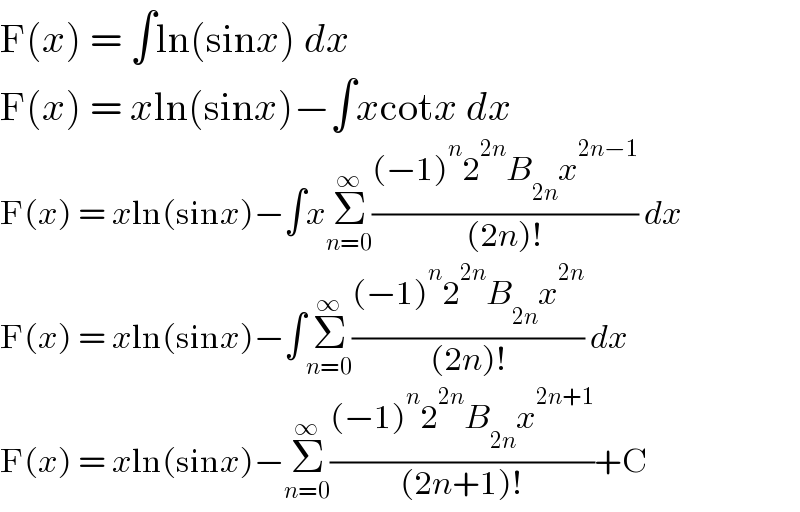
$$\mathrm{F}\left({x}\right)\:=\:\int\mathrm{ln}\left(\mathrm{sin}{x}\right)\:{dx} \\ $$$$\mathrm{F}\left({x}\right)\:=\:{x}\mathrm{ln}\left(\mathrm{sin}{x}\right)−\int{x}\mathrm{cot}{x}\:{dx} \\ $$$$\mathrm{F}\left({x}\right)\:=\:{x}\mathrm{ln}\left(\mathrm{sin}{x}\right)−\int{x}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} \mathrm{2}^{\mathrm{2}{n}} {B}_{\mathrm{2}{n}} {x}^{\mathrm{2}{n}−\mathrm{1}} }{\left(\mathrm{2}{n}\right)!}\:{dx} \\ $$$$\mathrm{F}\left({x}\right)\:=\:{x}\mathrm{ln}\left(\mathrm{sin}{x}\right)−\int\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} \mathrm{2}^{\mathrm{2}{n}} {B}_{\mathrm{2}{n}} {x}^{\mathrm{2}{n}} }{\left(\mathrm{2}{n}\right)!}\:{dx} \\ $$$$\mathrm{F}\left({x}\right)\:=\:{x}\mathrm{ln}\left(\mathrm{sin}{x}\right)−\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} \mathrm{2}^{\mathrm{2}{n}} {B}_{\mathrm{2}{n}} {x}^{\mathrm{2}{n}+\mathrm{1}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!}+\mathrm{C} \\ $$
