Question Number 183123 by SANOGO last updated on 21/Dec/22

$$\int{ln}\left({tanx}\right){dx} \\ $$
Answered by TheSupreme last updated on 21/Dec/22
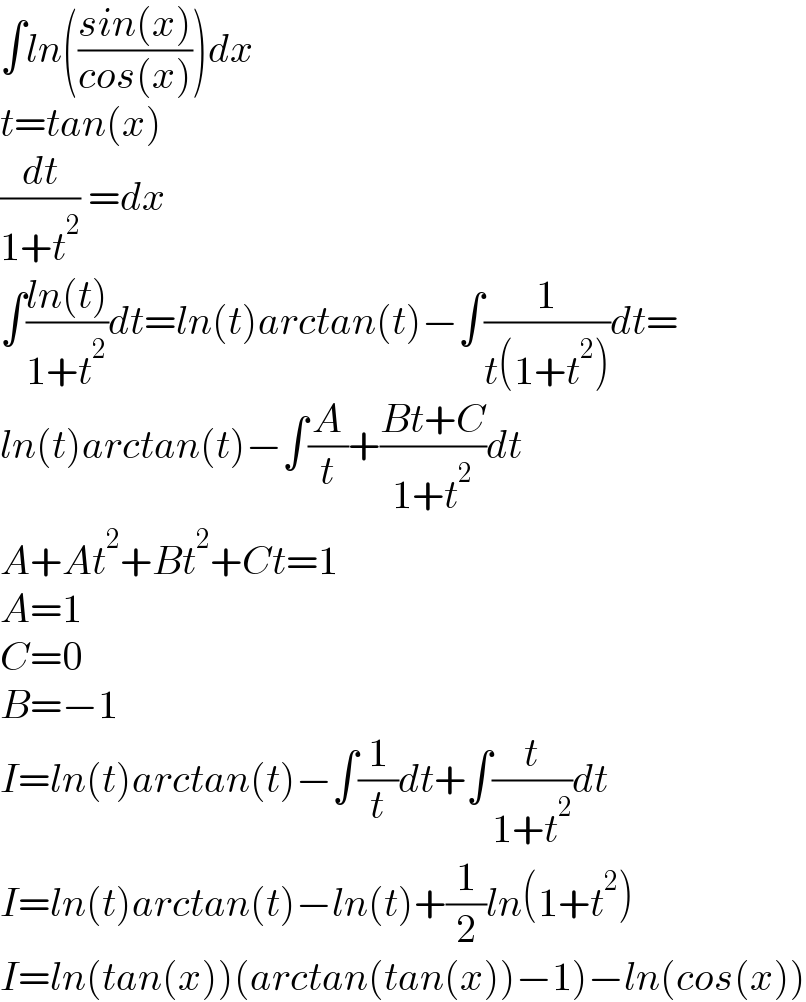
$$\int{ln}\left(\frac{{sin}\left({x}\right)}{{cos}\left({x}\right)}\right){dx} \\ $$$${t}={tan}\left({x}\right) \\ $$$$\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:={dx} \\ $$$$\int\frac{{ln}\left({t}\right)}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}={ln}\left({t}\right){arctan}\left({t}\right)−\int\frac{\mathrm{1}}{{t}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}{dt}= \\ $$$${ln}\left({t}\right){arctan}\left({t}\right)−\int\frac{{A}}{{t}}+\frac{{Bt}+{C}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$$${A}+{At}^{\mathrm{2}} +{Bt}^{\mathrm{2}} +{Ct}=\mathrm{1} \\ $$$${A}=\mathrm{1} \\ $$$${C}=\mathrm{0} \\ $$$${B}=−\mathrm{1} \\ $$$${I}={ln}\left({t}\right){arctan}\left({t}\right)−\int\frac{\mathrm{1}}{{t}}{dt}+\int\frac{{t}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$$${I}={ln}\left({t}\right){arctan}\left({t}\right)−{ln}\left({t}\right)+\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{1}+{t}^{\mathrm{2}} \right) \\ $$$${I}={ln}\left({tan}\left({x}\right)\right)\left({arctan}\left({tan}\left({x}\right)\right)−\mathrm{1}\right)−{ln}\left({cos}\left({x}\right)\right) \\ $$
Commented by MJS_new last updated on 21/Dec/22

$$\mathrm{wrong}.\:\mathrm{why}\:\mathrm{does}\:\mathrm{noone}\:\mathrm{test}\:\mathrm{their}\:\mathrm{results}\:\mathrm{anymore}? \\ $$$$\int\frac{\mathrm{ln}\:{t}}{{t}^{\mathrm{2}} +\mathrm{1}}{dt}= \\ $$$$\:\:\:\:\:{u}'=\frac{\mathrm{1}}{{t}^{\mathrm{2}} +\mathrm{1}}\:\rightarrow\:{u}=\mathrm{arctan}\:{t} \\ $$$$\:\:\:\:\:{v}=\mathrm{ln}\:{t}\:\rightarrow\:{v}'=\frac{\mathrm{1}}{{t}} \\ $$$$\:\:\:\:\:\int{u}'{v}={uv}−\int{uv}' \\ $$$$=\mathrm{ln}\:{t}\:\mathrm{arctan}\:{t}\:−\int\frac{\mathrm{arctan}\:{t}}{{t}}{dt} \\ $$
Commented by SANOGO last updated on 21/Dec/22

$${merci}\:{bien} \\ $$
