Menu Close

ln-x-1-x-dx-

Tinku Tara 0 Comments
Pin




Question Number 40467 by gunawan last updated on 22/Jul/18
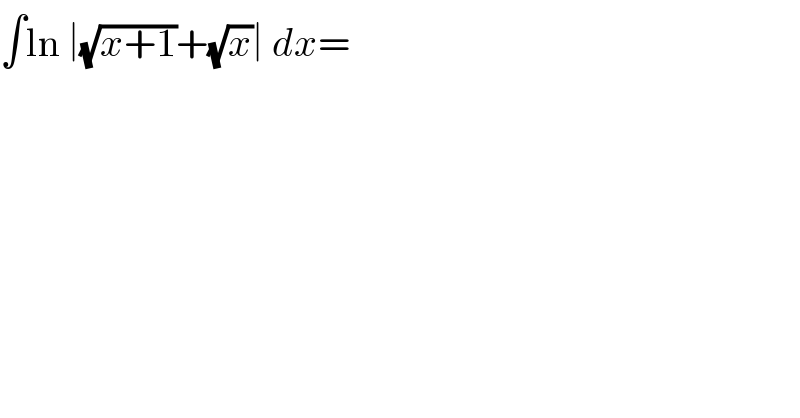
∫ln ∣(√(x+1))+(√x)∣ dx=
$$\int\mathrm{ln}\:\mid\sqrt{{x}+\mathrm{1}}+\sqrt{{x}}\mid\:{dx}= \\ $$
Commented by maxmathsup by imad last updated on 22/Jul/18
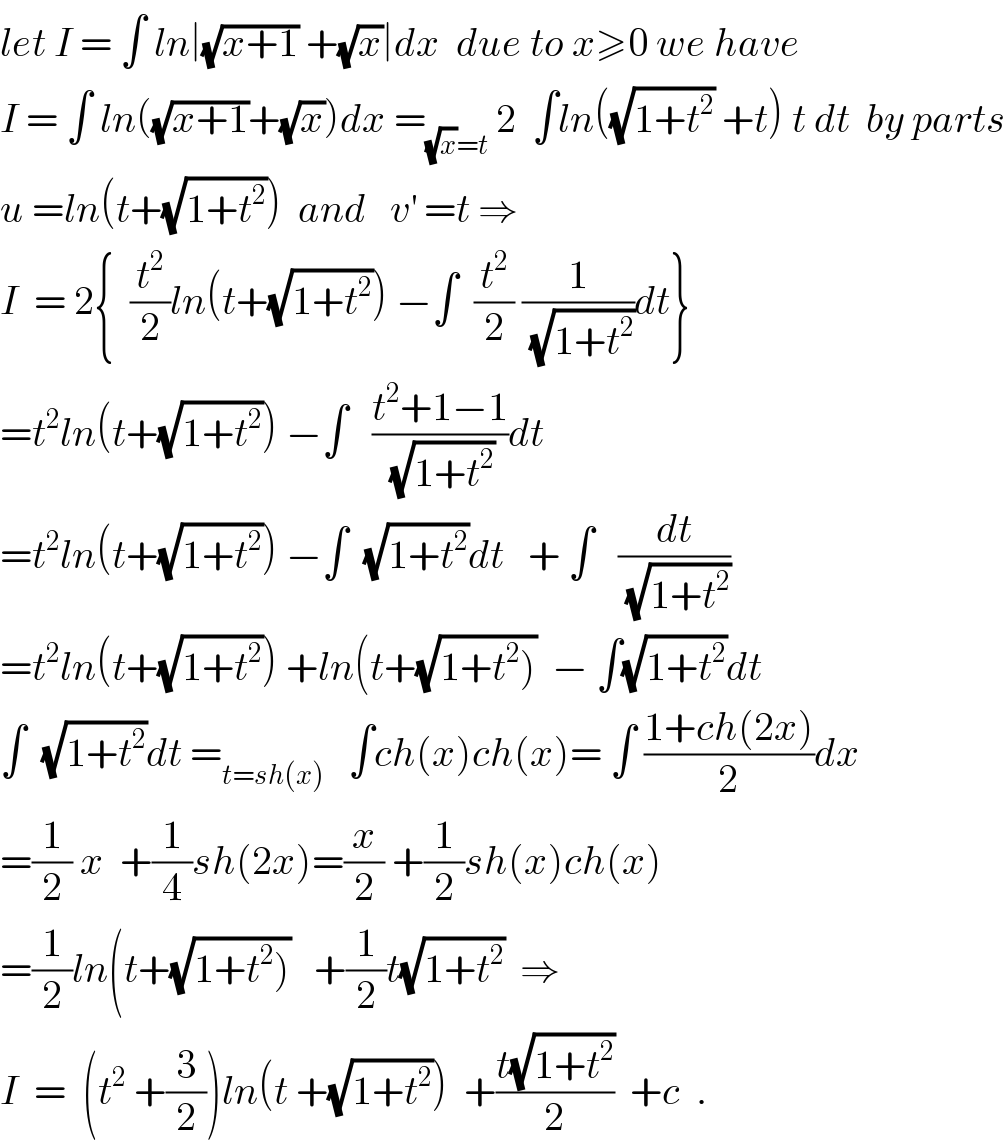
let I = ∫ ln∣(√(x+1)) +(√x)∣dx due to x≥0 we have I = ∫ ln((√(x+1))+(√x))dx =_((√x)=t) 2 ∫ln((√(1+t^2 )) +t) t dt by parts u =ln(t+(√(1+t^2 ))) and v^′ =t ⇒ I = 2{ (t^2 /2)ln(t+(√(1+t^2 ))) −∫ (t^2 /2) (1/( (√(1+t^2 ))))dt} =t^2 ln(t+(√(1+t^2 ))) −∫ ((t^2 +1−1)/( (√(1+t^2 ))))dt =t^2 ln(t+(√(1+t^2 ))) −∫ (√(1+t^2 ))dt + ∫ (dt/( (√(1+t^2 )))) =t^2 ln(t+(√(1+t^2 ))) +ln(t+(√(1+t^2 ))) − ∫(√(1+t^2 ))dt ∫ (√(1+t^2 ))dt =_(t=sh(x)) ∫ch(x)ch(x)= ∫ ((1+ch(2x))/2)dx =(1/2) x +(1/4)sh(2x)=(x/2) +(1/2)sh(x)ch(x) =(1/2)ln(t+(√(1+t^2 ))) +(1/2)t(√(1+t^2 )) ⇒ I = (t^2 +(3/2))ln(t +(√(1+t^2 ))) +((t(√(1+t^2 )))/2) +c .
$${let}\:{I}\:=\:\int\:{ln}\mid\sqrt{{x}+\mathrm{1}}\:+\sqrt{{x}}\mid{dx}\:\:{due}\:{to}\:{x}\geqslant\mathrm{0}\:{we}\:{have} \\ $$$${I}\:=\:\int\:{ln}\left(\sqrt{{x}+\mathrm{1}}+\sqrt{{x}}\right){dx}\:=_{\sqrt{{x}}={t}} \:\mathrm{2}\:\:\int{ln}\left(\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }\:+{t}\right)\:{t}\:{dt}\:\:{by}\:{parts} \\ $$$${u}\:={ln}\left({t}+\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }\right)\:\:{and}\:\:\:{v}^{'} \:={t}\:\Rightarrow \\ $$$${I}\:\:=\:\mathrm{2}\left\{\:\:\frac{{t}^{\mathrm{2}} }{\mathrm{2}}{ln}\left({t}+\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }\right)\:−\int\:\:\frac{{t}^{\mathrm{2}} }{\mathrm{2}}\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }}{dt}\right\} \\ $$$$={t}^{\mathrm{2}} {ln}\left({t}+\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }\right)\:−\int\:\:\:\frac{{t}^{\mathrm{2}} +\mathrm{1}−\mathrm{1}}{\:\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }}{dt} \\ $$$$={t}^{\mathrm{2}} {ln}\left({t}+\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }\right)\:−\int\:\:\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }{dt}\:\:\:+\:\int\:\:\:\frac{{dt}}{\:\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }} \\ $$$$={t}^{\mathrm{2}} {ln}\left({t}+\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }\right)\:+{ln}\left({t}+\sqrt{\left.\mathrm{1}+{t}^{\mathrm{2}} \right)}\:\:−\:\int\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }{dt}\right. \\ $$$$\int\:\:\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }{dt}\:=_{{t}={sh}\left({x}\right)} \:\:\:\int{ch}\left({x}\right){ch}\left({x}\right)=\:\int\:\frac{\mathrm{1}+{ch}\left(\mathrm{2}{x}\right)}{\mathrm{2}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:{x}\:\:+\frac{\mathrm{1}}{\mathrm{4}}{sh}\left(\mathrm{2}{x}\right)=\frac{{x}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{2}}{sh}\left({x}\right){ch}\left({x}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({t}+\sqrt{\left.\mathrm{1}+{t}^{\mathrm{2}} \right)}\:\:\:+\frac{\mathrm{1}}{\mathrm{2}}{t}\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }\:\:\Rightarrow\right. \\ $$$${I}\:\:=\:\:\left({t}^{\mathrm{2}} \:+\frac{\mathrm{3}}{\mathrm{2}}\right){ln}\left({t}\:+\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }\right)\:\:+\frac{{t}\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }}{\mathrm{2}}\:\:+{c}\:\:. \\ $$
Commented by math khazana by abdo last updated on 22/Jul/18
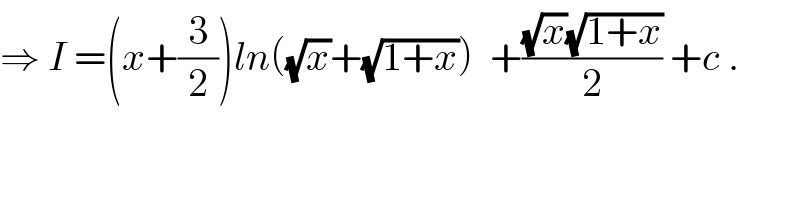
⇒ I =(x+(3/2))ln((√x)+(√(1+x))) +(((√x)(√(1+x)))/2) +c .
$$\Rightarrow\:{I}\:=\left({x}+\frac{\mathrm{3}}{\mathrm{2}}\right){ln}\left(\sqrt{{x}}+\sqrt{\mathrm{1}+{x}}\right)\:\:+\frac{\sqrt{{x}}\sqrt{\mathrm{1}+{x}}}{\mathrm{2}}\:+{c}\:. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 22/Jul/18
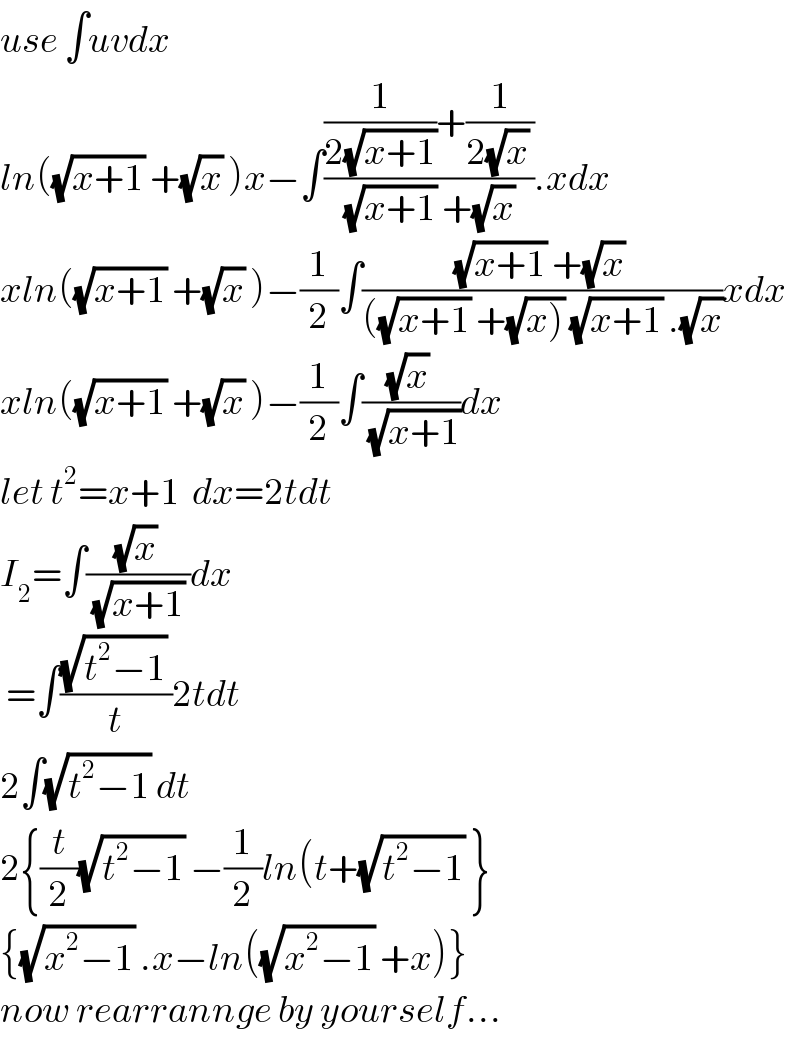
use ∫uvdx ln((√(x+1)) +(√x) )x−∫(((1/(2(√(x+1))))+(1/(2(√x) )))/( (√(x+1)) +(√x) )).xdx xln((√(x+1)) +(√x) )−(1/2)∫(((√(x+1)) +(√x) )/(((√(x+1)) +(√(x))) (√(x+1)) .(√x)))xdx xln((√(x+1)) +(√x) )−(1/2)∫(((√x) )/( (√(x+1))))dx let t^2 =x+1 dx=2tdt I_2 =∫(((√x) )/( (√(x+1)) ))dx =∫(((√(t^2 −1)) )/t)2tdt 2∫(√(t^2 −1)) dt 2{(t/2)(√(t^2 −1)) −(1/2)ln(t+(√(t^2 −1)) } {(√(x^2 −1)) .x−ln((√(x^2 −1)) +x)} now rearrannge by yourself...
$${use}\:\int{uvdx} \\ $$$${ln}\left(\sqrt{{x}+\mathrm{1}}\:+\sqrt{{x}}\:\right){x}−\int\frac{\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}+\mathrm{1}}}+\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}}\:}}{\:\sqrt{{x}+\mathrm{1}}\:+\sqrt{{x}}\:}.{xdx} \\ $$$${xln}\left(\sqrt{{x}+\mathrm{1}}\:+\sqrt{{x}}\:\right)−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\sqrt{{x}+\mathrm{1}}\:+\sqrt{{x}}\:}{\left(\sqrt{{x}+\mathrm{1}}\:+\sqrt{\left.{x}\right)}\:\sqrt{{x}+\mathrm{1}}\:.\sqrt{{x}}\right.}{xdx} \\ $$$${xln}\left(\sqrt{{x}+\mathrm{1}}\:+\sqrt{{x}}\:\right)−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\sqrt{{x}}\:}{\:\sqrt{{x}+\mathrm{1}}}{dx} \\ $$$${let}\:{t}^{\mathrm{2}} ={x}+\mathrm{1}\:\:{dx}=\mathrm{2}{tdt} \\ $$$${I}_{\mathrm{2}} =\int\frac{\sqrt{{x}}\:}{\:\sqrt{{x}+\mathrm{1}}\:}{dx} \\ $$$$\:=\int\frac{\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}\:}{{t}}\mathrm{2}{tdt} \\ $$$$\mathrm{2}\int\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}\:{dt} \\ $$$$\mathrm{2}\left\{\frac{{t}}{\mathrm{2}}\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}\:−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({t}+\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}\:\right\}\right. \\ $$$$\left\{\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\:.{x}−{ln}\left(\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\:+{x}\right)\right\} \\ $$$${now}\:{rearrannge}\:{by}\:{yourself}… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *