Menu Close

ln-x-ln-1-x-ln-1-2x-dx-

Tinku Tara 0 Comments
Pin




Question Number 63883 by mmkkmm000m last updated on 10/Jul/19
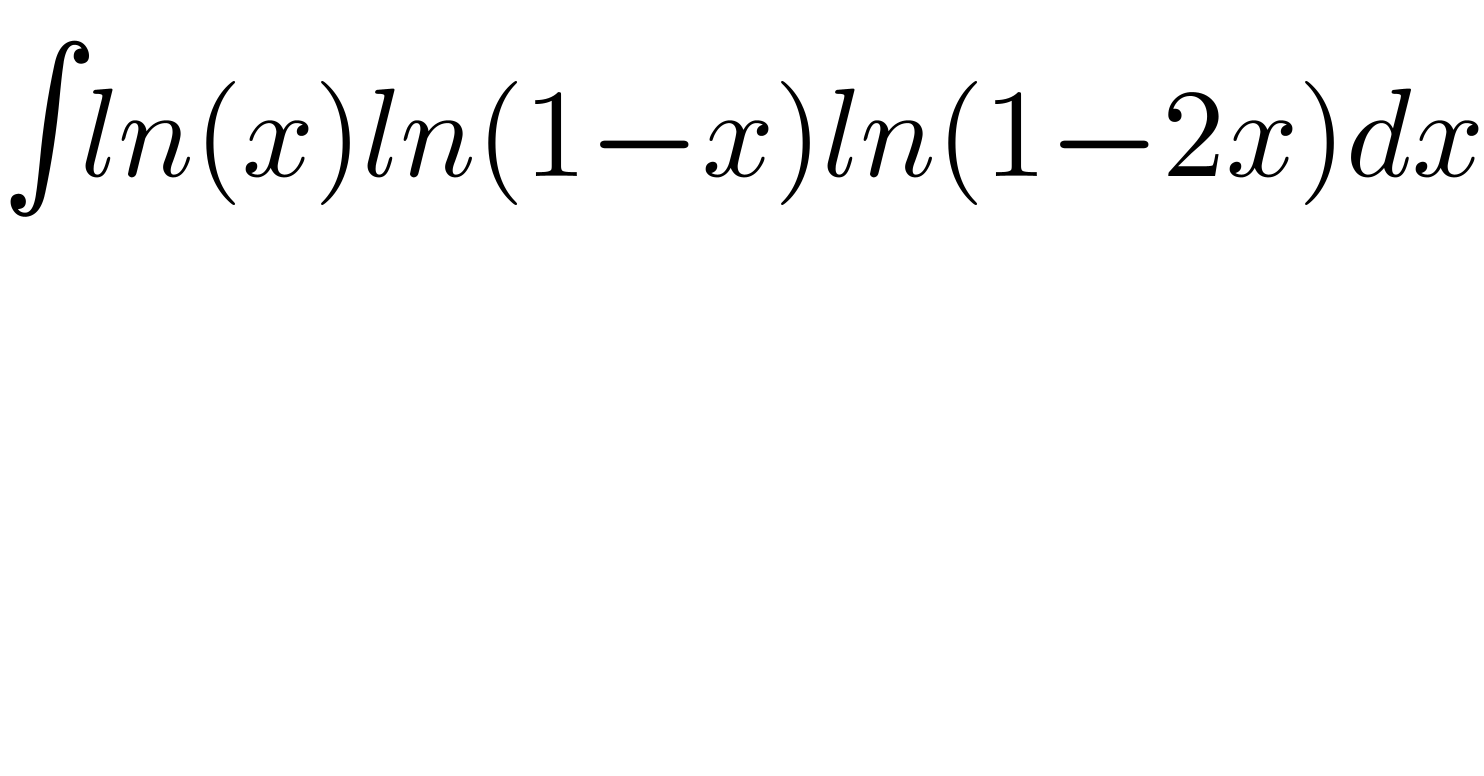
∫ln(x)ln(1−x)ln(1−2x)dx
$$\int{ln}\left({x}\right){ln}\left(\mathrm{1}−{x}\right){ln}\left(\mathrm{1}−\mathrm{2}{x}\right){dx} \\ $$
Commented by mathmax by abdo last updated on 12/Jul/19
let A =∫ ln(x)ln(1−x)ln(1−2x) dx we have ln^′ (1−u) =−(1/(1−u)) =−Σ_(n=0) ^∞ u^n ⇒ln(1−u) =−Σ_(n=0) ^∞ (u^(n+1) /(n+1)) +c(c=0) =−Σ_(n=1) ^∞ (u^n /n) ( ∣u∣<1) ⇒for ∣x∣<(1/2) we get ln(1−2x) =−Σ_(n=1) ^∞ ((2^n x^n )/n) and ln(1−x) =−Σ_(n=1) ^∞ (x^n /n) ⇒ ln(1−x)ln(1−2x) =(Σ_(n=1) ^∞ (2^n /n)x^n ).(Σ_(n=1) ^∞ (x^n /n)) =Σ_(n=1) ^∞ c_n x^n with c_n =Σ_(i+j=n) a_i b_j =Σ_(i=1) ^n a_i b_(n−i) =Σ_(i=1) ^n (2^i /i) (1/(n−i)) ⇒ln(1−x)ln(1−2x) =Σ_(n=1) ^∞ (Σ_(i=1) ^n (2^i /(i(n−i))))x^n ⇒ ∫ ln(x)ln(1−x)ln(1−2x)dx =∫ lnx(Σ_(n=1) ^∞ Σ_(i=1) ^n (2^i /(i(n−i))))x^n dx =Σ_(n=1) ^∞ Σ_(i=1) ^n (2^i /(i(n−i))) ∫ x^n ln(x)dx +c W_n =∫ x^n ln(x)dx by parts W_n =(x^(n+1) /(n+1)) ln(x) −∫ (x^(n+1) /(n+1)) (dx/x) =(x^(n+1) /(n+1))ln(x)−(1/((n+1))) ∫ x^n dx =((x^(n+1) ln(x))/(n+1)) −(x^(n+1) /((n+1)^2 )) ⇒ ∫ln(x)ln(1−x)ln(1−2x)dx =Σ_(n=1) ^∞ Σ_(i=1) ^n (2^i /(i(n−i))) ((x^(n+1) ln(x))/(n+1)) −Σ_(n=1) ^∞ Σ_(i=1) ^n (2^i /(i(n−i)(n+1)^2 ))x^(n+1) +c
$${let}\:{A}\:=\int\:{ln}\left({x}\right){ln}\left(\mathrm{1}−{x}\right){ln}\left(\mathrm{1}−\mathrm{2}{x}\right)\:{dx}\:\:{we}\:{have} \\ $$$${ln}^{'} \left(\mathrm{1}−{u}\right)\:=−\frac{\mathrm{1}}{\mathrm{1}−{u}}\:=−\sum_{{n}=\mathrm{0}} ^{\infty} \:{u}^{{n}} \:\Rightarrow{ln}\left(\mathrm{1}−{u}\right)\:=−\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{u}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}\:+{c}\left({c}=\mathrm{0}\right) \\ $$$$=−\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{u}^{{n}} }{{n}}\:\:\:\:\:\:\left(\:\:\mid{u}\mid<\mathrm{1}\right)\:\Rightarrow{for}\:\mid{x}\mid<\frac{\mathrm{1}}{\mathrm{2}}\:{we}\:{get} \\ $$$${ln}\left(\mathrm{1}−\mathrm{2}{x}\right)\:=−\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{2}^{{n}} {x}^{{n}} }{{n}}\:\:{and}\:{ln}\left(\mathrm{1}−{x}\right)\:=−\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{x}^{{n}} }{{n}}\:\Rightarrow \\ $$$${ln}\left(\mathrm{1}−{x}\right){ln}\left(\mathrm{1}−\mathrm{2}{x}\right)\:=\left(\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{2}^{{n}} }{{n}}{x}^{{n}} \right).\left(\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{x}^{{n}} }{{n}}\right) \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \:{c}_{{n}} \:{x}^{{n}} \:\:{with}\:{c}_{{n}} =\sum_{{i}+{j}={n}} {a}_{{i}} {b}_{{j}} =\sum_{{i}=\mathrm{1}} ^{{n}} \:{a}_{{i}} {b}_{{n}−{i}} \\ $$$$=\sum_{{i}=\mathrm{1}} ^{{n}} \:\:\frac{\mathrm{2}^{{i}} }{{i}}\:\frac{\mathrm{1}}{{n}−{i}}\:\Rightarrow{ln}\left(\mathrm{1}−{x}\right){ln}\left(\mathrm{1}−\mathrm{2}{x}\right)\:=\sum_{{n}=\mathrm{1}} ^{\infty} \left(\sum_{{i}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{2}^{{i}} }{{i}\left({n}−{i}\right)}\right){x}^{{n}} \:\Rightarrow \\ $$$$\int\:{ln}\left({x}\right){ln}\left(\mathrm{1}−{x}\right){ln}\left(\mathrm{1}−\mathrm{2}{x}\right){dx}\:=\int\:{lnx}\left(\sum_{{n}=\mathrm{1}} ^{\infty} \sum_{{i}=\mathrm{1}} ^{{n}} \:\:\frac{\mathrm{2}^{{i}} }{{i}\left({n}−{i}\right)}\right){x}^{{n}} {dx} \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \sum_{{i}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{2}^{{i}} }{{i}\left({n}−{i}\right)}\:\int\:{x}^{{n}} \:{ln}\left({x}\right){dx}\:+{c} \\ $$$${W}_{{n}} =\int\:\:{x}^{{n}} \:{ln}\left({x}\right){dx}\:\:{by}\:{parts}\: \\ $$$${W}_{{n}} =\frac{{x}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}\:{ln}\left({x}\right)\:−\int\:\frac{{x}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}\:\frac{{dx}}{{x}}\:=\frac{{x}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}{ln}\left({x}\right)−\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)}\:\int\:{x}^{{n}} {dx} \\ $$$$=\frac{{x}^{{n}+\mathrm{1}} {ln}\left({x}\right)}{{n}+\mathrm{1}}\:−\frac{{x}^{{n}+\mathrm{1}} }{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\int{ln}\left({x}\right){ln}\left(\mathrm{1}−{x}\right){ln}\left(\mathrm{1}−\mathrm{2}{x}\right){dx}\: \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \:\sum_{{i}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{2}^{{i}} }{{i}\left({n}−{i}\right)}\:\frac{{x}^{{n}+\mathrm{1}} {ln}\left({x}\right)}{{n}+\mathrm{1}}\:−\sum_{{n}=\mathrm{1}} ^{\infty} \:\sum_{{i}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{2}^{{i}} }{{i}\left({n}−{i}\right)\left({n}+\mathrm{1}\right)^{\mathrm{2}} }{x}^{{n}+\mathrm{1}} \:+{c} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *