Question Number 19738 by Tinkutara last updated on 15/Aug/17

$$\mathrm{Locus}\:\mathrm{of}\:\mathrm{the}\:\mathrm{point}\:{z}\:\mathrm{satisfying}\:\mathrm{the} \\ $$$$\mathrm{equation}\:\mid{iz}\:−\:\mathrm{1}\mid\:+\:\mid{z}\:−\:{i}\mid\:=\:\mathrm{2}\:\mathrm{is} \\ $$
Commented by math khazana by abdo last updated on 22/Jun/18
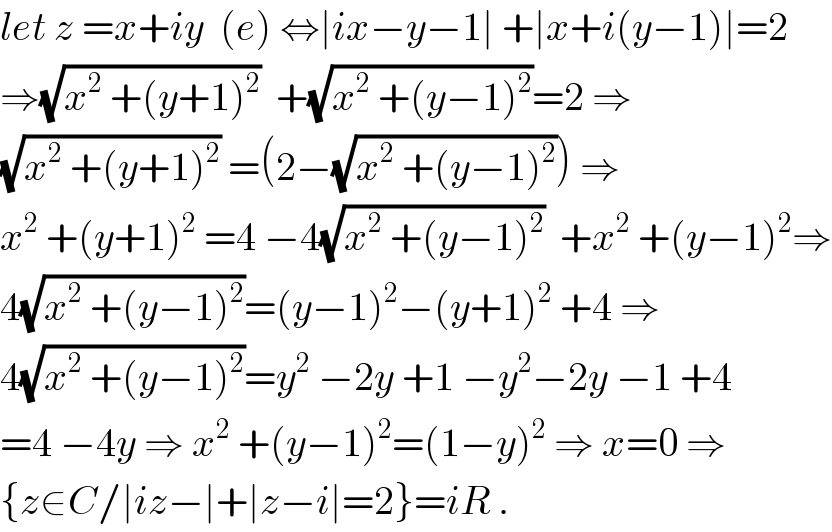
$${let}\:{z}\:={x}+{iy}\:\:\left({e}\right)\:\Leftrightarrow\mid{ix}−{y}−\mathrm{1}\mid\:+\mid{x}+{i}\left({y}−\mathrm{1}\right)\mid=\mathrm{2} \\ $$$$\Rightarrow\sqrt{{x}^{\mathrm{2}} \:+\left({y}+\mathrm{1}\right)^{\mathrm{2}} }\:\:+\sqrt{{x}^{\mathrm{2}} \:+\left({y}−\mathrm{1}\right)^{\mathrm{2}} }=\mathrm{2}\:\Rightarrow \\ $$$$\sqrt{{x}^{\mathrm{2}} \:+\left({y}+\mathrm{1}\right)^{\mathrm{2}} }\:=\left(\mathrm{2}−\sqrt{{x}^{\mathrm{2}} \:+\left({y}−\mathrm{1}\right)^{\mathrm{2}} }\right)\:\Rightarrow \\ $$$${x}^{\mathrm{2}} \:+\left({y}+\mathrm{1}\right)^{\mathrm{2}} \:=\mathrm{4}\:−\mathrm{4}\sqrt{{x}^{\mathrm{2}} \:+\left({y}−\mathrm{1}\right)^{\mathrm{2}} }\:\:+{x}^{\mathrm{2}} \:+\left({y}−\mathrm{1}\right)^{\mathrm{2}} \Rightarrow \\ $$$$\mathrm{4}\sqrt{{x}^{\mathrm{2}} \:+\left({y}−\mathrm{1}\right)^{\mathrm{2}} }=\left({y}−\mathrm{1}\right)^{\mathrm{2}} −\left({y}+\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{4}\:\Rightarrow \\ $$$$\mathrm{4}\sqrt{{x}^{\mathrm{2}} \:+\left({y}−\mathrm{1}\right)^{\mathrm{2}} }={y}^{\mathrm{2}} \:−\mathrm{2}{y}\:+\mathrm{1}\:−{y}^{\mathrm{2}} −\mathrm{2}{y}\:−\mathrm{1}\:+\mathrm{4} \\ $$$$=\mathrm{4}\:−\mathrm{4}{y}\:\Rightarrow\:{x}^{\mathrm{2}} \:+\left({y}−\mathrm{1}\right)^{\mathrm{2}} =\left(\mathrm{1}−{y}\right)^{\mathrm{2}} \:\Rightarrow\:{x}=\mathrm{0}\:\Rightarrow \\ $$$$\left\{{z}\in{C}/\mid{iz}−\mid+\mid{z}−{i}\mid=\mathrm{2}\right\}={iR}\:. \\ $$
Answered by ajfour last updated on 15/Aug/17

$$\Rightarrow\:\:\:\:\mid\mathrm{z}+\mathrm{i}\mid+\mid\mathrm{z}−\mathrm{i}\mid=\mathrm{2} \\ $$$$\mathrm{ellipse}\:\mathrm{with}\:\mathrm{origin}\:\mathrm{as}\:\mathrm{centre}. \\ $$$$\mathrm{focii}\::\:\:\:\:\mathrm{z}_{\mathrm{1}} =−\mathrm{i}\:\:;\:\:\mathrm{z}_{\mathrm{2}} =\mathrm{i} \\ $$$$\:\:\:\:\mathrm{shall}\:\mathrm{try}\:\mathrm{yo}\:\mathrm{obtain}\:\mathrm{equation}\:\mathrm{in} \\ $$$$\mathrm{the}\:\mathrm{form}:\:\:\:\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{a}^{\mathrm{2}} }+\frac{\mathrm{y}^{\mathrm{2}} }{\mathrm{b}^{\mathrm{2}} }=\mathrm{1}\:… \\ $$$$\mathrm{if}\:\mathrm{equation}\:\mathrm{of}\:\mathrm{ellipse}\:\mathrm{be} \\ $$$$\:\:\:\mid\mathrm{z}−\mathrm{z}_{\mathrm{1}} \mid+\mid\mathrm{z}−\mathrm{z}_{\mathrm{2}} \mid=\mathrm{d} \\ $$$$\mathrm{with}\:\mathrm{z}_{\mathrm{1}} ,\:\mathrm{and}\:\mathrm{z}_{\mathrm{2}} \:\mathrm{being}\:\mathrm{focii} \\ $$$$\:\:\:\:\mathrm{then}\:\:\:\mathrm{2a}=\mathrm{d} \\ $$$$\mathrm{and}\:\:\:\:\mathrm{b}^{\mathrm{2}} =\mathrm{a}^{\mathrm{2}} −\frac{\mid\mathrm{z}_{\mathrm{1}} −\mathrm{z}_{\mathrm{2}} \mid^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\:\:\mathrm{so}\:\:\:\:\mathrm{eccentricity}\:\mathrm{e}=\frac{\mid\mathrm{z}_{\mathrm{1}} −\mathrm{z}_{\mathrm{2}} \mid}{\mathrm{d}}\:. \\ $$
Commented by ajfour last updated on 16/Aug/17

$${Here}\:{major}\:{axis}\:{is}\:{the}\:{Imaginary} \\ $$$${axis},\:{so}\:\mathrm{2}{b}={d}\:{and}\:{a}^{\mathrm{2}} ={b}^{\mathrm{2}} −\frac{\mid{z}_{\mathrm{1}} −{z}_{\mathrm{2}} \mid^{\mathrm{2}} }{\mathrm{4}} \\ $$$${d}=\mathrm{2}\:\:,\:{so}\:{b}=\mathrm{1}\:\:\:{z}_{\mathrm{1}} ={i}\:,\:\:{z}_{\mathrm{2}} =−{i} \\ $$$$\:\:{so}\:\:\:{a}^{\mathrm{2}} =\mathrm{1}−\frac{\mid\mathrm{2}{i}\mid^{\mathrm{2}} }{\mathrm{4}}\:=\mathrm{0} \\ $$$${hence}\:{ellipse}\:{with}\:{minor}\:{axis} \\ $$$${length}\:{zero}\:{and}\:{major}\:{axis}\:{length} \\ $$$${equal}\:{to}\:\mathrm{2}.\:{extends}\:{from}\:{z}=−{i}\:{to} \\ $$$${z}={i}\:,\:{a}\:{double}\:{line}\:{segment}. \\ $$$$\left({special}\:{case}\:{of}\:{ellipse}\right). \\ $$
Commented by Tinkutara last updated on 16/Aug/17

$$\mathrm{Sorry},\:\mathrm{I}\:\mathrm{checked}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{today}\:\mathrm{and} \\ $$$$\mathrm{it}\:\mathrm{was}\:\mathrm{given}\:\mathrm{a}\:\mathrm{straight}\:\mathrm{line}! \\ $$
Commented by Tinkutara last updated on 16/Aug/17

$$\mathrm{So}\:\mathrm{we}\:\mathrm{will}\:\mathrm{consider}\:\mathrm{it}\:\mathrm{ellipse}\:\mathrm{or}\:\mathrm{a}\:\mathrm{line}? \\ $$
Commented by ajfour last updated on 16/Aug/17

$${cant}\:{say}\:! \\ $$
