Question Number 81039 by jagoll last updated on 09/Feb/20
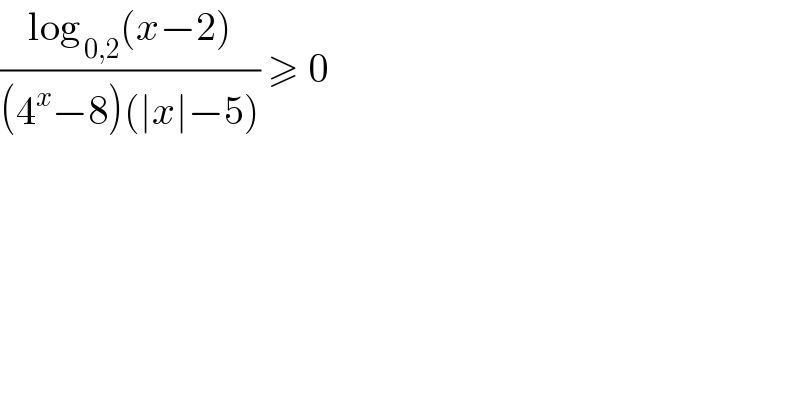
$$\frac{\mathrm{log}_{\:\mathrm{0},\mathrm{2}} \left({x}−\mathrm{2}\right)}{\left(\mathrm{4}^{{x}} −\mathrm{8}\right)\left(\mid{x}\mid−\mathrm{5}\right)}\:\geqslant\:\mathrm{0} \\ $$
Commented by john santu last updated on 09/Feb/20
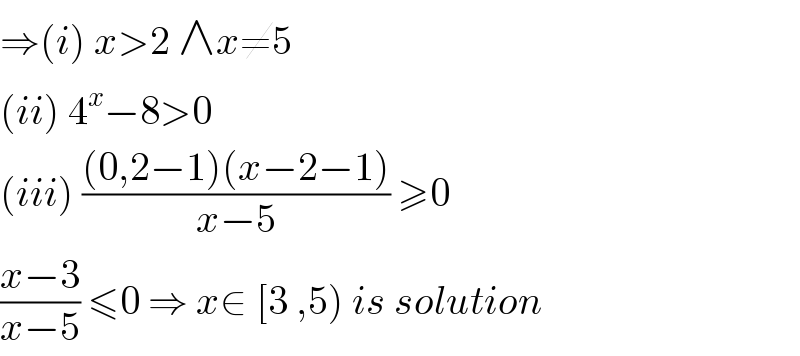
$$\Rightarrow\left({i}\right)\:{x}>\mathrm{2}\:\wedge{x}\neq\mathrm{5}\: \\ $$$$\left({ii}\right)\:\mathrm{4}^{{x}} −\mathrm{8}>\mathrm{0} \\ $$$$\left({iii}\right)\:\frac{\left(\mathrm{0},\mathrm{2}−\mathrm{1}\right)\left({x}−\mathrm{2}−\mathrm{1}\right)}{{x}−\mathrm{5}}\:\geqslant\mathrm{0} \\ $$$$\frac{{x}−\mathrm{3}}{{x}−\mathrm{5}}\:\leqslant\mathrm{0}\:\Rightarrow\:{x}\in\:\left[\mathrm{3}\:,\mathrm{5}\right)\:{is}\:{solution} \\ $$
Commented by jagoll last updated on 09/Feb/20
$${thanks}\:{you}\:{mister} \\ $$
