Question Number 85347 by jagoll last updated on 21/Mar/20
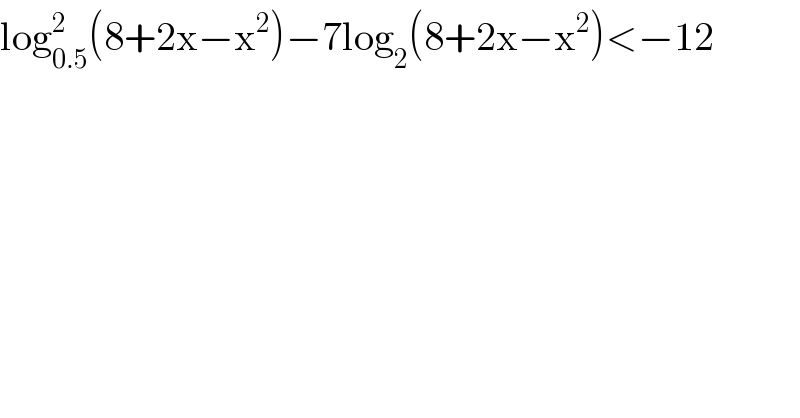
$$\mathrm{log}_{\mathrm{0}.\mathrm{5}} ^{\mathrm{2}} \left(\mathrm{8}+\mathrm{2x}−\mathrm{x}^{\mathrm{2}} \right)−\mathrm{7log}_{\mathrm{2}} \left(\mathrm{8}+\mathrm{2x}−\mathrm{x}^{\mathrm{2}} \right)<−\mathrm{12} \\ $$
Commented by john santu last updated on 21/Mar/20
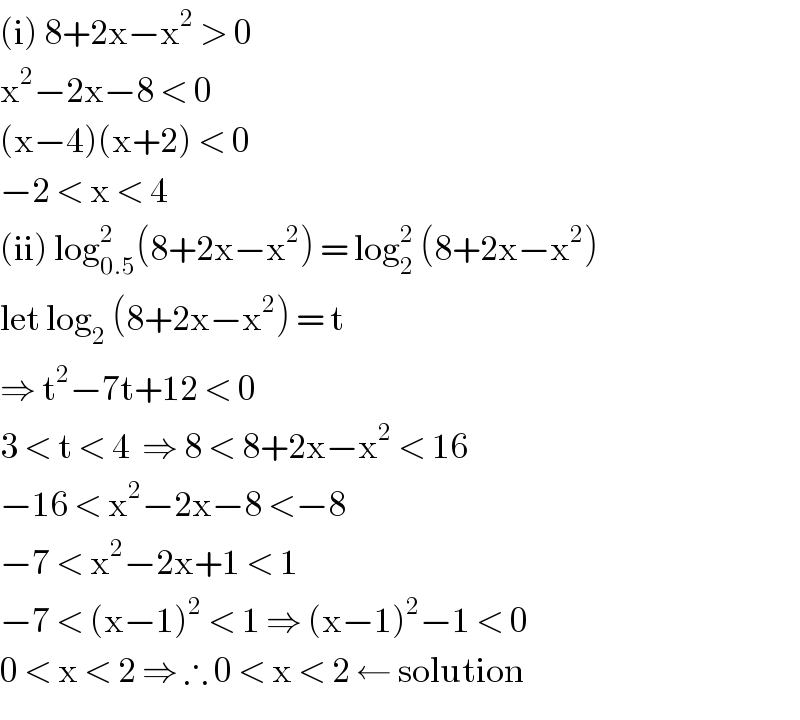
$$\left(\mathrm{i}\right)\:\mathrm{8}+\mathrm{2x}−\mathrm{x}^{\mathrm{2}} \:>\:\mathrm{0} \\ $$$$\mathrm{x}^{\mathrm{2}} −\mathrm{2x}−\mathrm{8}\:<\:\mathrm{0} \\ $$$$\left(\mathrm{x}−\mathrm{4}\right)\left(\mathrm{x}+\mathrm{2}\right)\:<\:\mathrm{0} \\ $$$$−\mathrm{2}\:<\:\mathrm{x}\:<\:\mathrm{4}\: \\ $$$$\left(\mathrm{ii}\right)\:\mathrm{log}_{\mathrm{0}.\mathrm{5}} ^{\mathrm{2}} \left(\mathrm{8}+\mathrm{2x}−\mathrm{x}^{\mathrm{2}} \right)\:=\:\mathrm{log}_{\mathrm{2}} ^{\mathrm{2}} \:\left(\mathrm{8}+\mathrm{2x}−\mathrm{x}^{\mathrm{2}} \right) \\ $$$$\mathrm{let}\:\mathrm{log}_{\mathrm{2}} \:\left(\mathrm{8}+\mathrm{2x}−\mathrm{x}^{\mathrm{2}} \right)\:=\:\mathrm{t} \\ $$$$\Rightarrow\:\mathrm{t}^{\mathrm{2}} −\mathrm{7t}+\mathrm{12}\:<\:\mathrm{0}\: \\ $$$$\mathrm{3}\:<\:\mathrm{t}\:<\:\mathrm{4}\:\:\Rightarrow\:\mathrm{8}\:<\:\mathrm{8}+\mathrm{2x}−\mathrm{x}^{\mathrm{2}} \:<\:\mathrm{16} \\ $$$$−\mathrm{16}\:<\:\mathrm{x}^{\mathrm{2}} −\mathrm{2x}−\mathrm{8}\:<−\mathrm{8} \\ $$$$−\mathrm{7}\:<\:\mathrm{x}^{\mathrm{2}} −\mathrm{2x}+\mathrm{1}\:<\:\mathrm{1} \\ $$$$−\mathrm{7}\:<\:\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} \:<\:\mathrm{1}\:\Rightarrow\:\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{1}\:<\:\mathrm{0} \\ $$$$\mathrm{0}\:<\:\mathrm{x}\:<\:\mathrm{2}\:\Rightarrow\:\therefore\:\mathrm{0}\:<\:\mathrm{x}\:<\:\mathrm{2}\:\leftarrow\:\mathrm{solution} \\ $$
