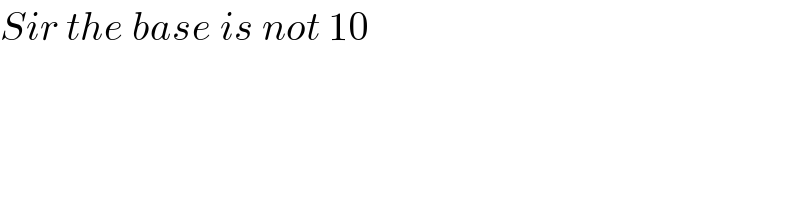Question Number 100832 by student work last updated on 28/Jun/20
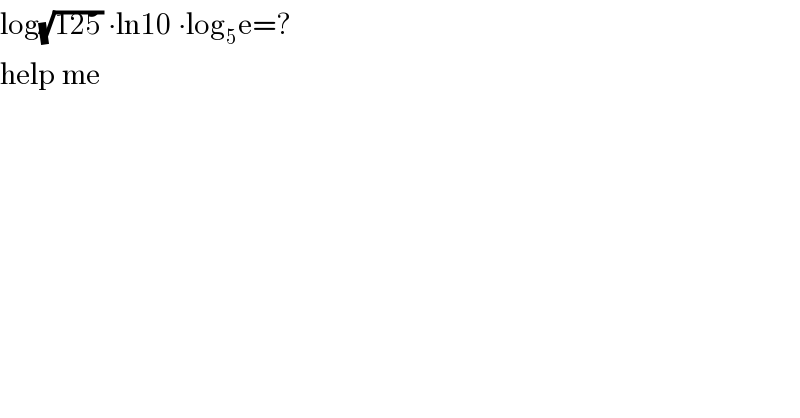
Commented by student work last updated on 28/Jun/20
Commented by student work last updated on 28/Jun/20

Commented by Dwaipayan Shikari last updated on 29/Jun/20
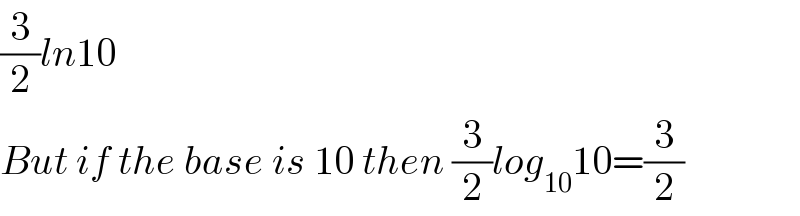
Answered by 1549442205 last updated on 29/Jun/20
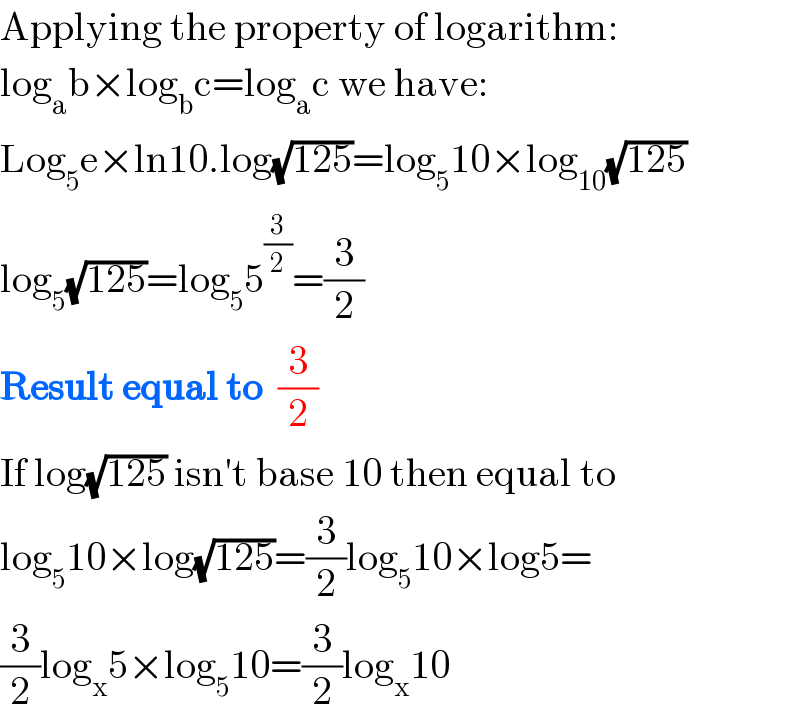
Commented by Dwaipayan Shikari last updated on 28/Jun/20