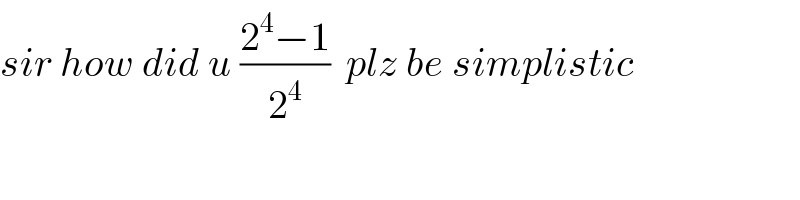log-2-2-2-2-2-

Question Number 19171 by gourav~ last updated on 06/Aug/17

{l o g}_{\sqrt{2}} \sqrt{2 \sqrt{2 \sqrt{2 \sqrt{2}}}}

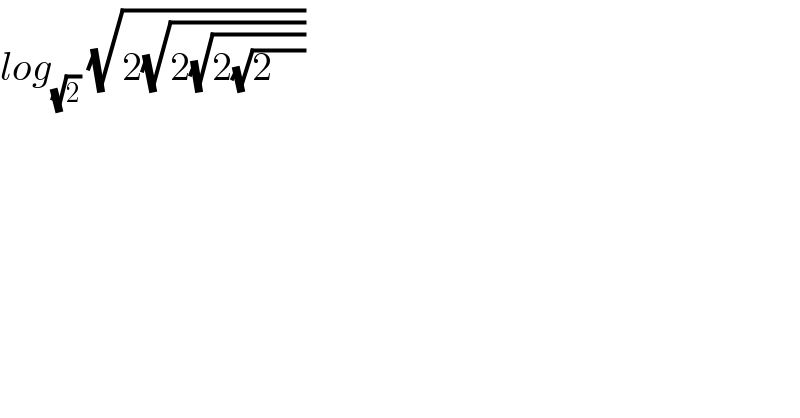
Commented by gourav~ last updated on 06/Aug/17

f i n d v a l u e

Answered by Tinkutara last updated on 06/Aug/17

\sqrt{2 \sqrt{2 \sqrt{2 \sqrt{2}}}} = 2^{\frac{2^{4} - 1}{2^{4}}} = 2^{\frac{15}{16}} = {(\sqrt{2})}^{\frac{15}{8}}

\log_{\sqrt{2}} {(\sqrt{2})}^{\frac{15}{8}} = \frac{15}{8}

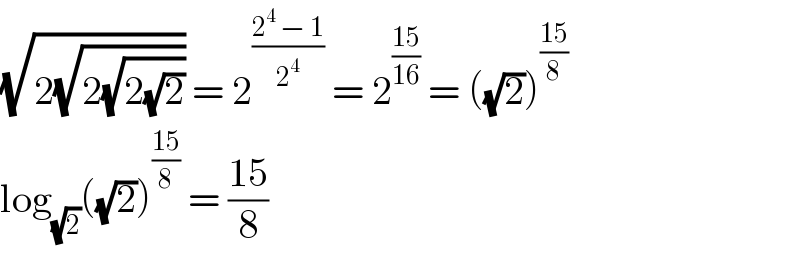
Commented by Tinkutara last updated on 06/Aug/17

See Q . 18551 .

Commented by chernoaguero@gmail.com last updated on 06/Aug/17

s i r h o w d i d u \frac{2^{4} - 1}{2^{4}} p l z b e s i m p l i s t i c