Question Number 89951 by john santu last updated on 20/Apr/20
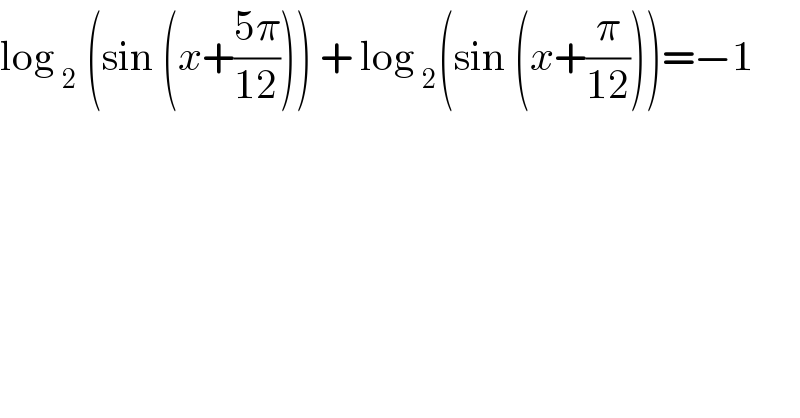
$$\mathrm{log}\:_{\mathrm{2}} \:\left(\mathrm{sin}\:\left({x}+\frac{\mathrm{5}\pi}{\mathrm{12}}\right)\right)\:+\:\mathrm{log}\:_{\mathrm{2}} \left(\mathrm{sin}\:\left({x}+\frac{\pi}{\mathrm{12}}\right)\right)=−\mathrm{1} \\ $$
Commented by jagoll last updated on 20/Apr/20

$$\Rightarrow\mathrm{sin}\:\left(\mathrm{x}+\frac{\mathrm{5}\pi}{\mathrm{12}}\right)\:\mathrm{sin}\:\left(\mathrm{x}+\frac{\pi}{\mathrm{12}}\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{cos}\:\left(\frac{\mathrm{4}\pi}{\mathrm{12}}\right)−\mathrm{cos}\:\left(\mathrm{2x}+\frac{\mathrm{6}\pi}{\mathrm{12}}\right)\:=\:\mathrm{1} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{cos}\:\left(\mathrm{2x}+\frac{\pi}{\mathrm{2}}\right)\:=\:\mathrm{1} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\:+\:\mathrm{sin}\:\mathrm{2x}\:=\:\mathrm{1}\:\Rightarrow\mathrm{sin}\:\mathrm{2x}\:=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\begin{cases}{\mathrm{2x}\:=\:\frac{\pi}{\mathrm{6}}+\mathrm{2n}\pi}\\{\mathrm{2x}\:=\:\frac{\mathrm{5}\pi}{\mathrm{6}}+\:\mathrm{2n}\pi}\end{cases} \\ $$$$\begin{cases}{\mathrm{x}\:=\:\frac{\pi}{\mathrm{12}}+\mathrm{n}\pi}\\{\mathrm{x}\:=\:\frac{\mathrm{5}\pi}{\mathrm{12}}+\mathrm{n}\pi}\end{cases} \\ $$$$ \\ $$
