Question Number 176748 by MASANJAJJ last updated on 26/Sep/22

$${log}_{\mathrm{4}} \sqrt{\mathrm{8}−{x}}=\mathrm{1}−{log}_{\mathrm{4}} {x} \\ $$$${solve}\:{for}\:{x} \\ $$
Answered by mr W last updated on 26/Sep/22

$$\mathrm{0}<{x}<\mathrm{8} \\ $$$$\mathrm{log}_{\mathrm{4}} \:\sqrt{\mathrm{8}−{x}}=\mathrm{log}_{\mathrm{4}} \:\frac{\mathrm{4}}{{x}} \\ $$$$\sqrt{\mathrm{8}−{x}}=\frac{\mathrm{4}}{{x}} \\ $$$$\mathrm{8}−{x}=\frac{\mathrm{16}}{{x}^{\mathrm{2}} } \\ $$$$\frac{\mathrm{1}}{{x}^{\mathrm{3}} }−\frac{\mathrm{1}}{\mathrm{2}{x}}+\frac{\mathrm{1}}{\mathrm{16}}=\mathrm{0} \\ $$$$\frac{\mathrm{1}}{{x}}=\frac{\mathrm{2}}{\:\sqrt{\mathrm{6}}}\:\mathrm{sin}\:\left(\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{3}\sqrt{\mathrm{6}}}{\mathrm{16}}+\frac{\mathrm{2}{k}\pi}{\mathrm{3}}\right),\:{k}=\mathrm{0},\mathrm{1}\:\left(\mathrm{2}\:{rejected}\right) \\ $$$$\Rightarrow{x}=\frac{\sqrt{\mathrm{6}}}{\mathrm{2}\:\mathrm{sin}\:\left(\frac{\mathrm{1}}{\mathrm{3}}\:\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{3}\sqrt{\mathrm{6}}}{\mathrm{16}}+\frac{\mathrm{2}{k}\pi}{\mathrm{3}}\right)},\:{k}=\mathrm{0},\mathrm{1} \\ $$
Commented by Tawa11 last updated on 27/Sep/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Answered by Rasheed.Sindhi last updated on 26/Sep/22
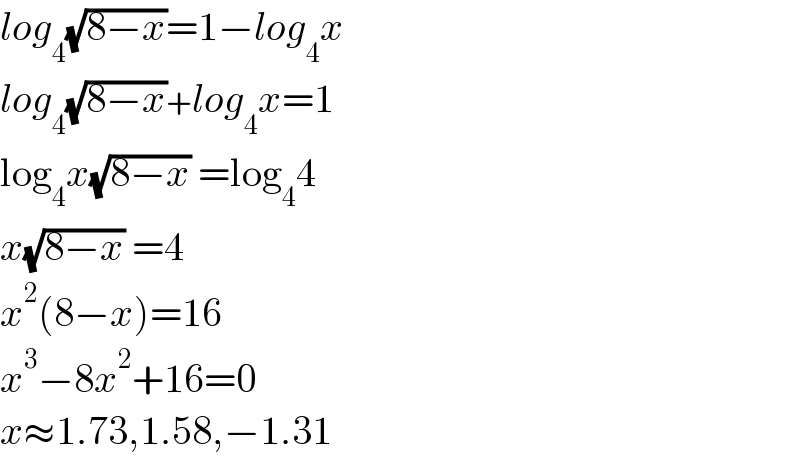
$${log}_{\mathrm{4}} \sqrt{\mathrm{8}−{x}}=\mathrm{1}−{log}_{\mathrm{4}} {x} \\ $$$${log}_{\mathrm{4}} \sqrt{\mathrm{8}−{x}}+{log}_{\mathrm{4}} {x}=\mathrm{1} \\ $$$$\mathrm{log}_{\mathrm{4}} {x}\sqrt{\mathrm{8}−{x}}\:=\mathrm{log}_{\mathrm{4}} \mathrm{4}\:\: \\ $$$${x}\sqrt{\mathrm{8}−{x}}\:=\mathrm{4} \\ $$$${x}^{\mathrm{2}} \left(\mathrm{8}−{x}\right)=\mathrm{16} \\ $$$${x}^{\mathrm{3}} −\mathrm{8}{x}^{\mathrm{2}} +\mathrm{16}=\mathrm{0} \\ $$$${x}\approx\mathrm{1}.\mathrm{73},\mathrm{1}.\mathrm{58},−\mathrm{1}.\mathrm{31} \\ $$
Commented by Rasheed.Sindhi last updated on 26/Sep/22

$$\boldsymbol{{Sir}},\:{this}\:{is}\:{what}\:{the}\:{calculator} \\ $$$$\:{calculates}.{ActuallyI}\:{feed}\:{x}^{\mathrm{3}} −\mathrm{8}{x}^{\mathrm{2}} +\mathrm{16}=\mathrm{0} \\ $$$${to}\:{the}\:{calculator}\:{instead}\:{of}\:{the}\:{original} \\ $$$${equation}! \\ $$
Commented by mr W last updated on 26/Sep/22

$${x}<\mathrm{0}\:{doesn}'{t}\:{fit}\:{the}\:{original}\:{equation}. \\ $$$${you}\:{meant}\:{x}\approx\mathrm{7}.\mathrm{73}? \\ $$
